题目内容
19.如果直线y=2x+m与两坐标轴围成的三角形面积等于m,则m的值是( )| A. | ±3 | B. | 3 | C. | ±4 | D. | 4 |
分析 求出直线与x和y轴的交点坐标,由三角形的面积=$\frac{1}{2}$|x||y|可得出关于m的方程,解出m的值即可.
解答 解:∵直线与x轴的交点为:(-$\frac{m}{2}$,0),与y轴的交点为:(0,m),
∴$\frac{1}{2}$|$\frac{m}{2}$|•|m|=m,解得m1=4,m2=0(不合题意).
故选D.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
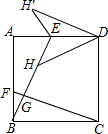 如图,正方形ABCD的边长为3,点E、F分别在边AD、AB上且AE=BF=1,连接BE、CF交于点G,在线段EG上取一点H使HG=BG,连接DH,把△EDH沿AD边翻折得到△EDH’,则点H到边DH’的距离是$\frac{24}{25}\sqrt{5}$.
如图,正方形ABCD的边长为3,点E、F分别在边AD、AB上且AE=BF=1,连接BE、CF交于点G,在线段EG上取一点H使HG=BG,连接DH,把△EDH沿AD边翻折得到△EDH’,则点H到边DH’的距离是$\frac{24}{25}\sqrt{5}$. 如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?
如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?