题目内容
3. 如图,在△ABC中,AB=AC,点D在AC上,AD=2CD,△ABC的周长为16,△ABD的周长比△CBD大4,求BC的长.
如图,在△ABC中,AB=AC,点D在AC上,AD=2CD,△ABC的周长为16,△ABD的周长比△CBD大4,求BC的长.
分析 设CD=x,然后根据△ABC的周长和△ABD与△CBD的周长的差列出方程组,再解方程组即可.
解答 解:设CD=x,则AD=2x,
∵△ABC的周长为16,
∴2(2x+x)+BC=16,
即6x+BC=16①,
∵△ABD的周长比△CBD大4,
∴(2x+x+2x+BD)-(x+BC+BD)=4,
即4x-BC=4②,
联立①②解得$\left\{\begin{array}{l}{x=2}\\{BC=4}\end{array}\right.$,
所以,BC的长为4.
点评 本题考查了等腰三角形的性质,三角形的周长的定义,读懂题目信息,考虑利用二元一次方程组求解更简便.

练习册系列答案
相关题目
12.计算(-3)×(-1)2的结果等于( )
| A. | 3 | B. | -2 | C. | -3 | D. | 1 |
13.Rt△ABC中,已知∠C=90°,AC=BC=4,以点A、B、C为圆心的圆分别记作圆A、圆B、圆C,这三个圆的半径长都等于2,那么下列结论正确的是( )
| A. | 圆A与圆B外离 | B. | 圆B与圆C外离 | C. | 圆A与圆C外离 | D. | 圆A与圆B相交 |
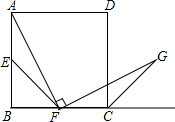 如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.
如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.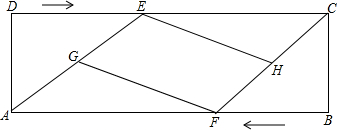
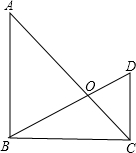 如图,已知△ABC和△BCD都是直角三角形,AB⊥BC,CD⊥BC,∠A=45°,∠D=60°,AC与BD交于点O,求∠BOC的度数.
如图,已知△ABC和△BCD都是直角三角形,AB⊥BC,CD⊥BC,∠A=45°,∠D=60°,AC与BD交于点O,求∠BOC的度数.