题目内容
16. 如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为2$\sqrt{5}$-2.
如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为2$\sqrt{5}$-2.
分析 根据题意得出抛物线解析式,进而表示出G点坐标,再利用2OF=FG,进而求出即可.
解答 解:∵正方形ABCD边长为4,
∴顶点坐标为:(0,4),B(2,0),
设抛物线解析式为:y=ax2+4,
将B点代入得,0=4a+4,
解得a=-1,
∴抛物线解析式为:y=-x2+4
设G点坐标为:(m,-m2+4),
则2m=-m2+4,
整理的:m2+2m-4=0,
解得:m1=-1+$\sqrt{5}$,a2=-1-$\sqrt{5}$(不合题意舍去),
∴正方形EFGH的边长FG=2m=2$\sqrt{5}$-2.
故答案为:2$\sqrt{5}$-2.
点评 此题主要考查了二次函数的综合应用以及一元二次方程的解法,根据正方形的性质以及抛物线上点的坐标性质得出等式是解题关键.

练习册系列答案
相关题目
8.下表是二次函数y=ax2+bx+c( a≠0)图象上部分点的横坐标(x)和纵坐标(y).
(1)观察表格,直接写出m=3;
(2)其中A(x1,y1)、B(x2,y2)在函数的图象上,且-1<x1<0,2<x2<3,则y1>y2(用“>”或“<”填空);
(3)求这个二次函数的表达式.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | m | 8 | … |
(2)其中A(x1,y1)、B(x2,y2)在函数的图象上,且-1<x1<0,2<x2<3,则y1>y2(用“>”或“<”填空);
(3)求这个二次函数的表达式.
 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
 请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0.
请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0.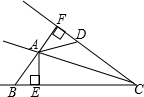 如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F. 如图,二次函数y=(x-h)2+k的顶点坐标为M(1,-4).
如图,二次函数y=(x-h)2+k的顶点坐标为M(1,-4).