题目内容
14.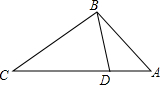 如图,点D在△ABC的边AC上,要判断△ADC与△ABC相似,添加一个条件,不正确的是( )
如图,点D在△ABC的边AC上,要判断△ADC与△ABC相似,添加一个条件,不正确的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | CB2=CD•CA | D. | AB2=AD•AC |
分析 由∠A是公共角,利用有两角对应相等的三角形相似,即可得A与B正确;又由两组对应边的比相等且夹角对应相等的两个三角形相似,即可得D正确,继而求得答案,注意排除法在解选择题中的应用.
解答 解:∵∠A是公共角,
∴当∠ABD=∠C或∠ADB=∠ABC时,△ADB∽△ABC(有两角对应相等的三角形相似);
故A与B正确;
当$\frac{AD}{AB}$=$\frac{AB}{AC}$时,即AB2=AD•AC,则△ADB∽△ABC(两组对应边的比相等且夹角对应相等的两个三角形相似);
故D正确;
当$\frac{CB}{CD}$=$\frac{AC}{BC}$时,∠A不是夹角,故不能判定△ADB与△ABC相似,
故C错误.
故选C.
点评 此题考查了相似三角形的判定.此题难度不大,注意掌握有两角对应相等的三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似定理的应用.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
5.若m>n,则下列不等式成立的是( )
| A. | -3m>-2n | B. | am>an | C. | a2m>a2n | D. | m-3>n-3 |
2.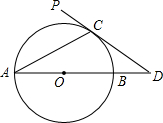 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )| A. | 2$\sqrt{2}$-2 | B. | 2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |
6.“2x-1=x+●”是一个被墨水污染过的方程,答案显示次方程的解是x=3,被墨水遮盖的是一个常数,则这个常数是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
4.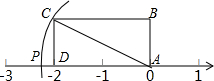 如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )
如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )
 如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )
如图,长方形ABCD的边AB=1,BC=2,AP=AC,则点P所表示的数是( )| A. | 5 | B. | -2.5 | C. | $\sqrt{5}$ | D. | $-\sqrt{5}$ |
 如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(-3,0),按要求解答下列问题.
如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(-3,0),按要求解答下列问题.