题目内容
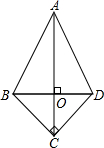 如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=
如图,四边形ABCD中,∠BCD=90°,BC=CD,对角线AC⊥BD于点O,若AD=| 2 |
∠ADC的度数为
考点:含30度角的直角三角形,等腰直角三角形
专题:
分析:根据等腰直角三角形的性质用OD表示出CD,再表示出AD,从而得到AD=OD,再根据直角三角形30°角所对的直角边等于斜边的一半求出∠OAD=30°,根据直角三角形两锐角互余求出∠ADO,再根据∠ADC=∠ADO+∠CDO代入数据计算即可得解.
解答:解:∵∠BCD=90°,BC=CD,
∴△BCD是等腰直角三角形,
∴CD=
OD,∠BDC=45°,
∵AD=
CD,
∴AD=
•
OD=2OD,
∵AC⊥BD,
∴∠OAD=30°,
∴∠ADO=90°-30°=60°,
∴∠ADC=∠ADO+∠CDO,
=60°+45°,
=105°.
故答案为:105°.
∴△BCD是等腰直角三角形,
∴CD=
| 2 |
∵AD=
| 2 |
∴AD=
| 2 |
| 2 |
∵AC⊥BD,
∴∠OAD=30°,
∴∠ADO=90°-30°=60°,
∴∠ADC=∠ADO+∠CDO,
=60°+45°,
=105°.
故答案为:105°.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半,等腰直角三角形的判定与性质,熟记各性质是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
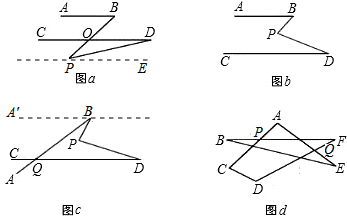
 如图,已知AB∥CD∥EF,∠BAC=120°,∠CEF=140°,则∠ACE=
如图,已知AB∥CD∥EF,∠BAC=120°,∠CEF=140°,则∠ACE=