题目内容
5. 如图.线段AB的端点坐标分别为A(-6,0),B(0,2).点c从(0,4)出发以每秒2个单位的速度沿直线y=4向左平移,同时线段AB也沿x轴的正方向以每秒3个单位的速度平移.则经过$\frac{12}{5}$秒,△ABC的周长最小.
如图.线段AB的端点坐标分别为A(-6,0),B(0,2).点c从(0,4)出发以每秒2个单位的速度沿直线y=4向左平移,同时线段AB也沿x轴的正方向以每秒3个单位的速度平移.则经过$\frac{12}{5}$秒,△ABC的周长最小.
分析 因为AB在平移的过程中长度不变,所以△ABC的周长的变化由AC与BC决定,所以作点B′关于直线y=4的对称点B″,连接A′B″交直线y=4于点C′,即C点恰好运动到C′的位置,
此时,△ABC的周长最小
解答 解:如下图所示:当点AB运动到A′B′的位置时,作点B′关于直线y=4的对称点B″,连接A′B″交直线y=4于点C′,即C点恰好运动到C′的位置,
因为,由对称的性质可知:B′C′=B″C′,而A′B″=A′C′+C′B″,
由“两点之间,线段最短”可知△ABC的周长最小.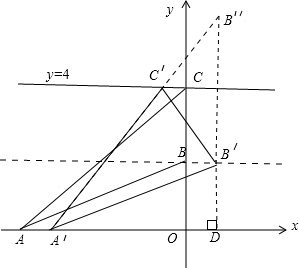
设此时运动的时间为t秒(t>0),则点A′(3t-6,0),B′(3t,2),C′(-2t,4),
根据题意,在Rt△A′DB″中,A′B″2=A′D2+B″D2,
(3t-3t+6)2+62=(-2t-3t+6)2+62,
(5t-6)2=36,
解得符合题意的t=$\frac{12}{5}$.
即:经过$\frac{12}{5}$秒时,△ABC的周长最小.
点评 本题考查了轴对称--最短路线问题,解题的关键是分析清楚△ABC的周长的变化规律,难点在于寻找点C′的位置.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.下列计算不正确的是( )
| A. | 2a÷a=2 | B. | a8÷a2=a4 | C. | ($\frac{1}{3}$)0×3=3 | D. | (2a3-a2)÷a2=2a-1 |
17.已知关于x的一元二次方程(m-1)x2-2mx+m+1=0的两个根都是正整数,则整数m的值是( )
| A. | 2 | B. | 3 | C. | 2或3 | D. | 1或2或3 |
14.估算$\sqrt{40}$的值是在( )
| A. | 5和6之间 | B. | 6和7之间 | C. | 7和8之间 | D. | 8和9之间 |
15.若a<b,则下列各不等式中一定成立的是( )
| A. | a-1<b-1 | B. | -a<-b | C. | $\frac{a}{3}>\frac{b}{3}$ | D. | ac<bc |

 在平面直角坐标系xOy中,直线y=kx+b的图象经过(1,0),(-2,3)两点,且与y轴交于点A.
在平面直角坐标系xOy中,直线y=kx+b的图象经过(1,0),(-2,3)两点,且与y轴交于点A. 若点O是边长为4的等边△ABC的外心,将一个边长足够大的正六边形的一个顶点固定在点O,使其绕点O旋转,在旋转的过程中,该正六边形与△ABC重叠部分的面积是$\frac{4\sqrt{3}}{3}$.
若点O是边长为4的等边△ABC的外心,将一个边长足够大的正六边形的一个顶点固定在点O,使其绕点O旋转,在旋转的过程中,该正六边形与△ABC重叠部分的面积是$\frac{4\sqrt{3}}{3}$.