题目内容
15.先化简,再求值:$\frac{1}{a+2b}$+$\frac{2{a}^{2}}{{a}^{2}-ab}$÷($\frac{3{b}^{2}}{a-b}$-a-b),其中a,b满足$\left\{\begin{array}{l}{a+b=3}\\{2a-b=0}\end{array}\right.$.
分析 首先解方程组求得a和b的值,然后化简所求的分式,化简时首先对括号内的分式通分相加,然后把除法转化为乘法,再计算加减即可化简,最后代入a和b的值计算即可.
解答 解:解方程组$\left\{\begin{array}{l}{a+b=3}\\{2a-b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,
原式=$\frac{1}{a+2b}$+$\frac{2{a}^{2}}{a(a-b)}$÷$\frac{3{b}^{2}-(a+b)(a-b)}{a-b}$
=$\frac{1}{a+2b}$+$\frac{2{a}^{2}}{a(a-b)}$÷$\frac{4{b}^{2}-{a}^{2}}{a-b}$
=$\frac{1}{a+2b}$+$\frac{2{a}^{2}}{a(a-b)}$•$\frac{a-b}{(2b+a)(2b-a)}$
=$\frac{1}{a+2b}$+$\frac{2}{(2b+a)(2b-a)}$
=$\frac{2b-a+2}{(2b+a)(2b-a)}$.
当$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$时,原式=$\frac{4-1+2}{(4+1)(4-1)}$=$\frac{5}{15}$=$\frac{1}{3}$.
点评 本题考查了分式的化简求值,先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
5.计算:5(6+1)(62+1)(64+1)+1,结果为( )
| A. | 616 | B. | 68 | C. | 68+1 | D. | 68-1 |
3.假设你班有男生24名,女生26名,班主任要从班里任选一名“社区服务”志愿者,则选中男生的概率是( )
| A. | $\frac{12}{25}$ | B. | $\frac{13}{25}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{50}$ |
20.$\frac{1}{2}$sin60°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\sqrt{3}$ |
7.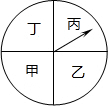 如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在丙区域内的概率是( )
如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在丙区域内的概率是( )
 如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在丙区域内的概率是( )
如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在丙区域内的概率是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
5.盐城城市快速路网是我市建市史上单项投资规模最大的城市交通工程建设项目,计划2016年底建成通车,项目预算投资130亿元,130亿用科学记数法表示为( )
| A. | 130×108 | B. | 1.3×109 | C. | 1.3×1010 | D. | 1.3×1011 |