题目内容
13.甲、乙两人共同完成一项工程30天,甲先工作16天,乙再加入,两人合作15天后,甲因为有事退出,乙单独做了12天后完成全部,如果甲单独做这项工程需要多少天?分析 设甲单独完成这项工程需要x天,乙单独完成这项工程需要y天,根据题意得到:甲、乙两人共同完成一项工程30天;甲工作31天,乙工作27天恰好完成这一项工程.由此列出方程组,利用换元法解该二元一次方程组即可.
解答 解:设甲单独完成这项工程需要x天,乙单独完成这项工程需要y天,根据题意得
$\left\{\begin{array}{l}{\frac{30}{x}+\frac{30}{y}=1}\\{\frac{31}{x}+\frac{27}{y}=1}\end{array}\right.$.
设a=$\frac{1}{x}$,b=$\frac{1}{y}$,则原方程组转化为:$\left\{\begin{array}{l}{30a+30b=1}\\{31a+27b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{40}}\\{b=\frac{1}{120}}\end{array}\right.$,
所以$\left\{\begin{array}{l}{x=40}\\{y=120}\end{array}\right.$,
经检验$\left\{\begin{array}{l}{x=40}\\{y=120}\end{array}\right.$是原方程组的解.
答:甲单独完成这项工程需要40天.
点评 本题考查了二元一次方程组的应用.解题关键是弄清题意,合适的等量关系,列出方程组.

练习册系列答案
相关题目
3.关于x的方程5x+m-2=2x的解为正数,则m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | m<2 |
4. 某初中学校欲从三名候选学生中向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不舍弃权票),每得一票记一分,投票结果统计如图所示;其次,对三名候选学生进行了面试,成绩如表所示.
某初中学校欲从三名候选学生中向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不舍弃权票),每得一票记一分,投票结果统计如图所示;其次,对三名候选学生进行了面试,成绩如表所示.
请你根据以上信息解答下列问题:
(1)请根据扇形图计算每名候选学生的民主投票得分;
(2)若投票、面试两项得分按照6:4的比例计算成绩,则应该录用谁?
 某初中学校欲从三名候选学生中向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不舍弃权票),每得一票记一分,投票结果统计如图所示;其次,对三名候选学生进行了面试,成绩如表所示.
某初中学校欲从三名候选学生中向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不舍弃权票),每得一票记一分,投票结果统计如图所示;其次,对三名候选学生进行了面试,成绩如表所示.| 候选学生 | 甲 | 乙 | 丙 |
| 面试成绩 | 95 | 80 | 85 |
(1)请根据扇形图计算每名候选学生的民主投票得分;
(2)若投票、面试两项得分按照6:4的比例计算成绩,则应该录用谁?
 如图,⊙O直径AB=13cm,C为⊙O上的一点,已知CD⊥AB,垂足为D,并且CD=6cm,AD<DB,求AD的长.
如图,⊙O直径AB=13cm,C为⊙O上的一点,已知CD⊥AB,垂足为D,并且CD=6cm,AD<DB,求AD的长. 如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.
如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.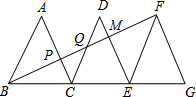 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,则BP=1.
如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,则BP=1. 如图,等腰梯形ABCD是⊙O的外切四边形,AD∥BC,AB=10,则等腰梯形ABCD的周长为40.
如图,等腰梯形ABCD是⊙O的外切四边形,AD∥BC,AB=10,则等腰梯形ABCD的周长为40.