题目内容
2.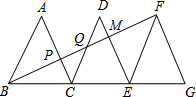 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,则BP=1.
如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1,则BP=1.
分析 由题意得出FG=$\sqrt{3}$,GE=1,BG=3,则$\frac{FG}{BG}$=$\frac{EG}{FG}$,再由∠FGE=∠BGF,得△BFG∽△FEG,根据△BFG∽△FEG,得$\frac{FG}{BG}$=$\frac{FE}{BF}$,再由FG=FE,求出BF,根据全等三角形性质得到∠ACB=∠G,于是得到AC∥FG,得到比例式$\frac{BP}{BF}=\frac{BC}{BG}$=$\frac{1}{3}$,即可得到结果.
解答 解:∵△ABC、△DCE、△FEG是三个全等的等腰三角形,
∴FG=AB=$\sqrt{3}$,GE=BC=1,BG=3BC=3,
∴$\frac{FG}{BG}$=$\frac{\sqrt{3}}{3}$,$\frac{EG}{FG}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{FG}{BG}$=$\frac{EG}{FG}$,
∵∠FGE=∠BGF,
∴△BFG∽△FEG;
∴$\frac{FG}{BG}$=$\frac{FE}{BF}$
∵FG=FE,
∴BF=BG=3;
∵∠ACB=∠G,
∴AC∥FG,
∴$\frac{BP}{BF}=\frac{BC}{BG}$=$\frac{1}{3}$,
∴BP=$\frac{1}{3}$BF=1.
故答案为:1.
点评 本题主要考查了平行线分线段定理,以及三角形相似的判定,正确理解AB∥CD∥EF,AC∥DE∥FG是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 某Wi-Fi热点的信号覆盖区域是以这个Wi-Fi热点为圆心,r为半径的圆(包括圆的内部),如图为某广场的平面示意图,16个长25m,宽15m的展区排列在面积为9600m2的矩形ABCD区域,展区间纵向横向的每条路宽均相等.
某Wi-Fi热点的信号覆盖区域是以这个Wi-Fi热点为圆心,r为半径的圆(包括圆的内部),如图为某广场的平面示意图,16个长25m,宽15m的展区排列在面积为9600m2的矩形ABCD区域,展区间纵向横向的每条路宽均相等.