题目内容
5.先化简,再求值:(1-$\frac{1}{x+2}$)÷$\frac{{x}^{2}-1}{x+2}$,其中x=3tan30°+2cos60°.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x+1}{x+2}$•$\frac{x+2}{(x+1)(x-1)}$
=$\frac{1}{x-1}$,
∵x=3×$\frac{\sqrt{3}}{3}$+2×$\frac{1}{2}$=$\sqrt{3}$+1,
∴原式=$\frac{1}{\sqrt{3}+1-1}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
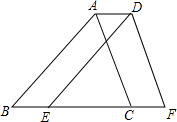 如图,将周长为5的△ABC沿BC方向平移了1个单位长度得到△DEF,连接AD,则四边形ABFD的周长为( )
如图,将周长为5的△ABC沿BC方向平移了1个单位长度得到△DEF,连接AD,则四边形ABFD的周长为( ) 如图,连接A、B两地间的高速公路全长为120千米,在AB上建有两个收费站C,D,已知AC:CB=1:5,AD:DB=11:1,一辆小车从C站到D站行驶了$\frac{3}{4}$小时,则小车的速度是每小时120千米.
如图,连接A、B两地间的高速公路全长为120千米,在AB上建有两个收费站C,D,已知AC:CB=1:5,AD:DB=11:1,一辆小车从C站到D站行驶了$\frac{3}{4}$小时,则小车的速度是每小时120千米. 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=3,AF=4,∠EAF=60°,求四边形ABCD的面积.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=3,AF=4,∠EAF=60°,求四边形ABCD的面积.