题目内容
7.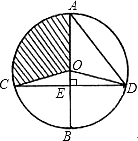 如图,⊙O的直径AB⊥弦CD,垂足为E,连接AD、OC、OD,且OD=5.
如图,⊙O的直径AB⊥弦CD,垂足为E,连接AD、OC、OD,且OD=5.(1)若CD=8,求AD长;
(2)若∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留π).
分析 (1)由垂径定理得出DE=$\frac{1}{2}$CD=4,由勾股定理求出OE,得出AE,再由勾股定理求出AD即可;
(2)设∠ADO=4x,则∠EDO=x,由等腰三角形的性质得出∠OAD=∠ADO=4x,由直角三角形的性质得出方程,解方程求出∠ADC=50°,由圆周角定理得出∠AOC=100°,由扇形面积公式即可得出结果.
解答 解:(1)∵直径AB⊥弦CD,
∴DE=$\frac{1}{2}$CD=4,
由勾股定理得:OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=3,
∴AE=5+3=8,
∴AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=4$\sqrt{5}$;
(2)设∠ADO=4x,则∠EDO=x,
∵OA=OD,
∴∠OAD=∠ADO=4x,
∵AB⊥CD,
∴∠AED=90°,
∴∠OAD+∠ADE=90°,
即4x+4x+x=90°,
解得:x=10°,
∴∠ADC=50°,
∴∠AOC=100°,
∴扇形OAC(阴影部分)的面积=$\frac{100×π×{5}^{2}}{360}$=$\frac{125π}{18}$.
点评 本题考查了垂径定理、勾股定理、等腰三角形的性质、圆周角定理、扇形面积的计算;熟练掌握垂径定理和勾股定理,由圆周角定理求出∠AOC是解决(2)的关键.

练习册系列答案
相关题目
2.小明根据柸州市出租车的收费标准,制定了打车费计算的数值转换机示意图:

(1)根据数值转换机程序计算下列乘客应付打车费用:
(2)通过填写表格,用一句话描述你的发现:当乘车的里程大于2公里时,乘车费用随着乘车的里程增大而增大
(3)请用代数式表示上述数值转换程序.

(1)根据数值转换机程序计算下列乘客应付打车费用:
| 乘客 | 甲 | 乙 | 丙 | 丁 | 戍 |
| 输入/公里 | 1.5 | 2 | 4 | 6 | 8 |
| 输出/元 | 5 | 5 | 8 | 11 | 14 |
(3)请用代数式表示上述数值转换程序.
12. 如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )
如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )
 如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )
如图,l1∥l2∥l3,AB=3,BC=2,EF=3,则DF的长为( )| A. | 3 | B. | 5.5 | C. | 6.5 | D. | 7.5 |
16.下列交通标志是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
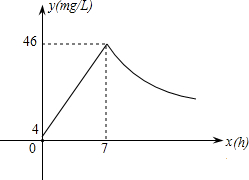 近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题:
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题: