题目内容
16.下列交通标志是轴对称图形的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据轴对称图形的概念求解,如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
解答 解:A、不是轴对称图形,不符合题意;
B、不是轴对称图形,不符合题意;
C、不是轴对称图形,不符合题意;
D、是轴对称图形,对称轴有两条,符合题意.
故选:D.
点评 本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.

练习册系列答案
相关题目
6.用配方法解方程x2-4x-3=0时,原方程变形为( )
| A. | (x-2)2=7 | B. | (x+2)2=7 | C. | (x-2)2=4 | D. | (x+2)2=1 |
11.探索与应用.先填写下表,通过观察后再回答问题:
(1)表格中x=0.1;y=10;
(2)从表格中探究a与$\sqrt{a}$数位的规律,并利用这个规律解决下面两个问题:
①已知$\sqrt{10}$≈3.16,则$\sqrt{1000}$≈31.62;②已知$\sqrt{3.24}$=1.8,若$\sqrt{a}$=180,则a=32400;
(3)拓展:已知$\root{3}{12}≈2.289$,若$\root{3}{x}=0.2289$,则z=0.012.
| a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| $\sqrt{a}$ | … | 0.01 | x | 1 | y | 100 | … |
(2)从表格中探究a与$\sqrt{a}$数位的规律,并利用这个规律解决下面两个问题:
①已知$\sqrt{10}$≈3.16,则$\sqrt{1000}$≈31.62;②已知$\sqrt{3.24}$=1.8,若$\sqrt{a}$=180,则a=32400;
(3)拓展:已知$\root{3}{12}≈2.289$,若$\root{3}{x}=0.2289$,则z=0.012.
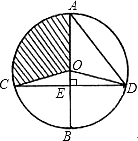 如图,⊙O的直径AB⊥弦CD,垂足为E,连接AD、OC、OD,且OD=5.
如图,⊙O的直径AB⊥弦CD,垂足为E,连接AD、OC、OD,且OD=5.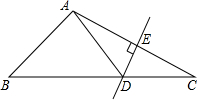 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABC的周长为21cm,则△ABD的周长为13 cm.
如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABC的周长为21cm,则△ABD的周长为13 cm. 如图,在△ABC中,∠C=28°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A=96°.
如图,在△ABC中,∠C=28°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A=96°.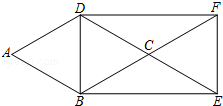 如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,连接DB,BE,EF,FD.
如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,连接DB,BE,EF,FD.