题目内容
17.求下列函数的最大值(或最小值)和对应的自变量x的值(1)y=x2-3x+2
(2)y=-2x2+$\sqrt{2}$x-1.
分析 (1)利用配方法求得函数的最值与自变量x的值即可;
(2)利用公式法求得函数的最值与自变量x的值即可.
解答 解:(1)∵y=x2-3x+2=(x-$\frac{3}{2}$)2-$\frac{1}{4}$,
∴当x=$\frac{3}{2}$时,函数的最小值为-$\frac{1}{4}$.
(2)y=-2x2+$\sqrt{2}$x-1,
∵a=-2,b=$\sqrt{2}$,c=-1,
∴当x=-$\frac{\sqrt{2}}{-4}$=$\frac{\sqrt{2}}{4}$时,函数取得最大值为$\frac{4×(-2)×(-1)-(\sqrt{2})^{2}}{-2×4}$=-$\frac{3}{4}$.
点评 此题考查二次函数的最值,求二次函数的最值一般利用公式法或配方法解决问题

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12.$\sqrt{{a}^{2}}$等于( )
| A. | a | B. | -a | C. | ±a | D. | 以上都不对 |
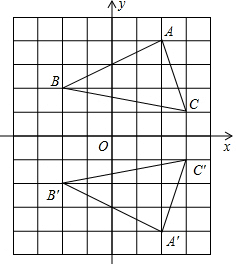 (1)如图所示,写出直角坐标系中△ABC与△A′B′C′各点的坐标,并判断这两个三角形是通过怎样的变化得到的;
(1)如图所示,写出直角坐标系中△ABC与△A′B′C′各点的坐标,并判断这两个三角形是通过怎样的变化得到的;