题目内容
16. 如图所示,A,O,B三点共线,BC是⊙O的切线,切点为B,OC平行于弦AD,求证:DC是⊙O的切线.
如图所示,A,O,B三点共线,BC是⊙O的切线,切点为B,OC平行于弦AD,求证:DC是⊙O的切线.
分析 连接OD、OB,易证△OBC≌△ODC,则∠OBC=∠ODC,由BC是⊙O的切线,可知∠OBC=∠ODC=90°,故DC是⊙O的切线.
解答 证明:连接OD、OB;
∵OA=OD,
∴∠A=∠ADO,
∵AD∥OC,
∴∠A=∠BOC,∠ADO=∠COD,
∴∠BOC=∠COD.
在△OBC和△ODC中,
$\left\{\begin{array}{l}{OB=OD}\\{∠BOC=∠COD}\\{OC=OC}\end{array}\right.$,
∴△OBC≌△ODC,
∴∠OBC=∠ODC,又BC是⊙O的切线,
∴∠OBC=90°,
∴∠ODC=90°,
∴DC是⊙O的切线.
点评 本题考查切线的性质和判定及圆周角定理的综合运用,证明△OBC≌△ODC是解决问题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
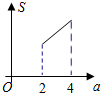
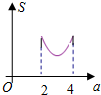
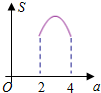
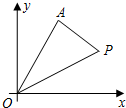 如图,平面直角坐标中,A点坐标为(1,2),P点坐标为(a,2a-3),其中2≤a≤4,设△OAP的面积为S,则S与a的函数图象大致为( )
如图,平面直角坐标中,A点坐标为(1,2),P点坐标为(a,2a-3),其中2≤a≤4,设△OAP的面积为S,则S与a的函数图象大致为( )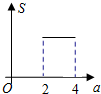
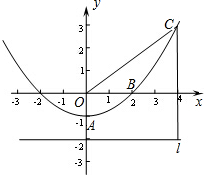 如图,已知抛物线y=ax2+c经过A(0,-1)和B(2,0),在x轴下方有一直线l,它的解析式是y=-2(即l上每点的纵坐标都是-2).
如图,已知抛物线y=ax2+c经过A(0,-1)和B(2,0),在x轴下方有一直线l,它的解析式是y=-2(即l上每点的纵坐标都是-2).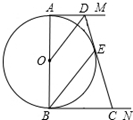 如图,已知AB是⊙O的直径,AM和BN是⊙O的两条切线,点E是⊙O上一点,点D是AM上一点,连接DE并延长交BN于点C,连接OD、BE,且OD∥BE.
如图,已知AB是⊙O的直径,AM和BN是⊙O的两条切线,点E是⊙O上一点,点D是AM上一点,连接DE并延长交BN于点C,连接OD、BE,且OD∥BE.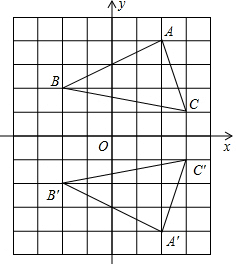 (1)如图所示,写出直角坐标系中△ABC与△A′B′C′各点的坐标,并判断这两个三角形是通过怎样的变化得到的;
(1)如图所示,写出直角坐标系中△ABC与△A′B′C′各点的坐标,并判断这两个三角形是通过怎样的变化得到的;