题目内容
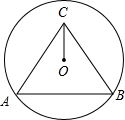如图，圆O过点B、C，圆心O在正△ABC的内部，AB=2| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
考点：垂径定理,等边三角形的性质,勾股定理
专题：
分析：延长CO交AB于点D，连接OA，根据勾股定理可求得CD的长，再在直角三角形AOD中，求得OA即可．
解答：
解：延长CO交AB于点D，连接OA，
∵△ABC为正三角，
∴CD⊥AB，
∵AB=2
，
∴AD=
，
∴CD=3，
∵OC=1，
∴OD=2，
∴OA=
=
，
故选D．
解：延长CO交AB于点D，连接OA，∵△ABC为正三角，
∴CD⊥AB，
∵AB=2
| 3 |
∴AD=
| 3 |
∴CD=3，
∵OC=1，
∴OD=2，
∴OA=
(
|
| 7 |
故选D．
点评：本题考查了垂径定理、等边三角形的性质以及勾股定理，考查了这几个知识点的综合运用．
练习册系列答案
相关题目
如图，⊙A的圆心A的坐标是（2，3），x轴与⊙A相切于点D，与y轴交于B，C两点，则cos∠ABC为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在我市开展的“好书伴我成长”读书活动中，某中学为了解八年级300名学生读书情况，随机调查了八年级50名学生读书的册数，统计数据如下表所示：
那么这50名同学读书册数的众数，中位数分别是（ ）
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
| A、3，2 | B、3，3 |
| C、2，3 | D、3，1 |
-2的相反数是（ ）
| A、2 | ||
| B、-|-2| | ||
C、
| ||
D、-
|
在菱形ABCD中，下列结论一定正确的是（ ）| A、AD=BD |
| B、菱形ABCD的面积是AC和BD的积 |
| C、∠DAC=∠BAC |
| D、∠ACB=30° |
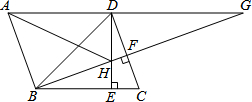如图，?ABCD中，∠DBC=45°，高线DE、BF交于点H，BF、AD的延长线交于点G；联结AH．