题目内容
7.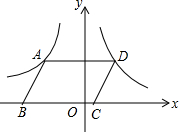 如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )| A. | -1 | B. | -2 | C. | -3 | D. | -5 |
分析 连接OA、OD,如图,利用平行四边形的性质得AD垂直y轴,则利用反比例函数的比例系数k的几何意义得到S△OAE和S△ODE,所以S△OAD=2,然后根据平行四边形的面积公式可得到?ABCD的面积=2S△OAD=4,即可求出k的值.
解答 解:连接OA、OD,如图,
∵四边形ABCD为平行四边形,
∴AD垂直y轴,
∴S△OAE=$\frac{1}{2}$×|k|=$\frac{|k|}{2}$,S△ODE=$\frac{1}{2}$×|1|=$\frac{1}{2}$,
∴S△OAD=$\frac{|k|}{2}$+$\frac{1}{2}$,
∵?ABCD的面积=2S△OAD=4.
∴|k|+1=4,
解得k=-3或3,
∵k<0.
∴k=-3
故C.
点评 本题考查了反比例函数比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.也考查了平行四边形的性质.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18.在Rt△ABC中,D为斜边AB的中点,且BC=3,AC=4,则线段CD的长是( )
| A. | 2 | B. | 3 | C. | $\frac{5}{2}$ | D. | 5 |
2.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{x+2y=2m-1}\\{2x-y=6}\end{array}\right.$的解满足x+y=-3,则m的值( )
| A. | -3 | B. | -1 | C. | 1 | D. | 2 |
12.甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)填写下表:
(2)从以下四个方面对甲、乙两城市的空气质量进行分析.
①从平均数和空气质量为优的次数来分析甲乙两城市的空气质量哪个好一些;
②从平均数和中位数来分析甲乙两城市的空气质量哪个好一些;
③从平均数和方差来分析甲乙两城市的空气质量变化情况;
④根据折线图上两城市空气污染指数的走势来分析甲乙两城市的空气质量哪个好一些.

(1)填写下表:
| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 85 | 1 |
| 乙 | 80 | 1060 | 80 | 3 |
①从平均数和空气质量为优的次数来分析甲乙两城市的空气质量哪个好一些;
②从平均数和中位数来分析甲乙两城市的空气质量哪个好一些;
③从平均数和方差来分析甲乙两城市的空气质量变化情况;
④根据折线图上两城市空气污染指数的走势来分析甲乙两城市的空气质量哪个好一些.
19.下列约分正确的是( )
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{a+c}{b+c}$=$\frac{a}{b}$ | C. | $\frac{a+b}{b+a}=0$ | D. | $\frac{x-y}{y-x}=-1$ |