题目内容
16.(1)计算:$\sqrt{9}$+$\root{3}{8}$-|1-$\sqrt{2}$|(2)解不等式:1-$\frac{2-3x}{5}$>$\frac{1+x}{2}$
(3)解不等式组:$\left\{\begin{array}{l}{3x-1≥x+1}\\{x+4<4x-2}\end{array}\right.$.
分析 (1)首先计算开方和绝对值,然后再计算加减即可;
(2)首先去分母,不等式两边同时乘以10,再去括号,移项,合并同类项即可;
(3)首先分别计算出两个不等式的解集,再根据大大取大确定不等式组的解集.
解答 解:(1)原式=3+2-($\sqrt{2}-$1)=3+2-$\sqrt{2}$+1=6-$\sqrt{2}$;
(2)去分母得:10-2(2-3x)>5(1+x),
去括号得:10-4+6x>5+5x,
移项得:6x-5x>5-10+4,
合并同类项得:x>-1;
(3)$\left\{\begin{array}{l}{3x-1≥x+1①}\\{x+4<4x-2②}\end{array}\right.$,
由①得:x≥
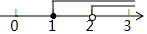
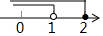
由②得:x>2,
不等式组的解集为x>2.
点评 此题主要考查了解一元一次不等式(组),以及实数的运算,关键是掌握解一元一次不等式与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1,掌握不等式组确定解集的方法:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
7.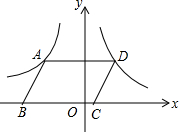 如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
 如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )| A. | -1 | B. | -2 | C. | -3 | D. | -5 |
4.下列说法正确的是( )
| A. | 负数有一个平方根 | |
| B. | $\frac{1}{4}$是0.5的一个平方根 | |
| C. | 72的平方根是7 | |
| D. | 正数有两个平方根,且这两个平方根之和等于0 |
11. 中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用(2,-1)表示“炮”的位置,那么“将”的位置应表示为( )
中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用(2,-1)表示“炮”的位置,那么“将”的位置应表示为( )
 中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用(2,-1)表示“炮”的位置,那么“将”的位置应表示为( )
中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用(2,-1)表示“炮”的位置,那么“将”的位置应表示为( )| A. | (-2,3) | B. | (0,-5) | C. | (-3,1) | D. | (-4,2) |
1.圆柱的侧面展开图不可能是( )
| A. | 正方形 | B. | 长方形 | C. | 菱形 | D. | 直角梯形 |