题目内容
18.在Rt△ABC中,D为斜边AB的中点,且BC=3,AC=4,则线段CD的长是( )| A. | 2 | B. | 3 | C. | $\frac{5}{2}$ | D. | 5 |
分析 根据勾股定理列式求出AB的长度,再根据直角三角形斜边上的中线等于斜边的一半解答.
解答 解:∵AC=4cm,BC=3,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵D为斜边AB的中点,
∴CD=$\frac{1}{2}$AB=$\frac{1}{2}$×5=$\frac{5}{2}$.
故选C.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的应用,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.数据17,19,17,18,21的中位数为( )
| A. | 17 | B. | 18 | C. | 18.5 | D. | 19 |
3.每年四月北京很多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰.据测定,杨絮纤维的直径约为0.000 010 5米,将0.000 010 5用科学记数法可表示为( )
| A. | 1.05×105 | B. | 1.05×10-5 | C. | 0.105×10-4 | D. | 10.5×10-6 |
7.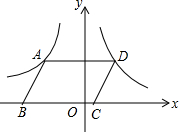 如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
 如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )| A. | -1 | B. | -2 | C. | -3 | D. | -5 |
1.圆柱的侧面展开图不可能是( )
| A. | 正方形 | B. | 长方形 | C. | 菱形 | D. | 直角梯形 |
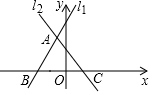 如图直线l1:y=2x+4与直线l2:y=-2x+2相交于点A,且直线l1,l2分别交x轴于点B和C.
如图直线l1:y=2x+4与直线l2:y=-2x+2相交于点A,且直线l1,l2分别交x轴于点B和C.