题目内容
15.计算:(1)(3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$)÷$\sqrt{32}$
(2)$\sqrt{12}$×$\sqrt{\frac{1}{6}}$-$\sqrt{8}$×$\frac{1}{\sqrt{2}+1}$.
分析 (1)首先把二次根式化简,然后把括号里面的二次根式合并,再计算除法即可;
(2)首先计算二次根式的乘法,然后计算减法即可.
解答 解:(1)原式=(9$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$)÷4$\sqrt{2}$,
=8$\sqrt{2}$$÷4\sqrt{2}$,
=2;
(2)原式=$\sqrt{12×\frac{1}{6}}$-$\sqrt{8}$×$\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}$,
=$\sqrt{2}$-$\sqrt{8}$×($\sqrt{2}$-1),
=$\sqrt{2}$-4+2$\sqrt{2}$,
=3$\sqrt{2}$-4.
点评 此题主要考查了二次根式的混合运算,关键是掌握二次根式的混合运算应注意以下几点:
①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.
②在运算中每个根式可以看做是一个“单项式“,多个不同类的二次根式的和可以看作“多项式“.

练习册系列答案
相关题目
3.每年四月北京很多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰.据测定,杨絮纤维的直径约为0.000 010 5米,将0.000 010 5用科学记数法可表示为( )
| A. | 1.05×105 | B. | 1.05×10-5 | C. | 0.105×10-4 | D. | 10.5×10-6 |
20.计算[(-a)2]3•(a3)2所得结果为( )
| A. | a10 | B. | -a10 | C. | a12 | D. | -a12 |
7.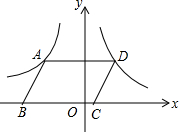 如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
 如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )
如图,在平面直角坐标系中,?ABCD的顶点B、C在x轴上,A、D两点分别在反比例函数y=$\frac{k}{x}$(k<0,x<0)与y=$\frac{1}{x}$(x>0)的图象上,若?ABCD的面积为4,则k的值为( )| A. | -1 | B. | -2 | C. | -3 | D. | -5 |
4.下列说法正确的是( )
| A. | 负数有一个平方根 | |
| B. | $\frac{1}{4}$是0.5的一个平方根 | |
| C. | 72的平方根是7 | |
| D. | 正数有两个平方根,且这两个平方根之和等于0 |