题目内容
20.有一面积为5$\sqrt{3}$的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为20$\sqrt{3}$和20.分析 分两种情形讨论①当30度角是等腰三角形的顶角,②当30度角是底角,分别作腰上的高即可.
解答 解: 如图1中,当∠A=30°,AB=AC时,设AB=AC=a,
如图1中,当∠A=30°,AB=AC时,设AB=AC=a,
作BD⊥AC于D,∵∠A=30°,
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$a,
∴$\frac{1}{2}$•a•$\frac{1}{2}$a=5$\sqrt{3}$,
∴a2=20$\sqrt{3}$,
∴△ABC的腰长为边的正方形的面积为20$\sqrt{3}$.
如图2中,当∠ABC=30°,AB=AC时,作BD⊥CA交CA的延长线于D,设AB=AC=a,
∵AB=AC,
∴∠ABC=∠C=30°,
∴∠BAC=120°,∠BAD=60°,
在RT△ABD中,∵∠D=90°,∠BAD=60°,
∴BD=$\frac{\sqrt{3}}{2}$a,
∴$\frac{1}{2}$•a•$\frac{\sqrt{3}}{2}$a=5$\sqrt{3}$,
∴a2=20,
∴△ABC的腰长为边的正方形的面积为20.
故答案为20$\sqrt{3}$或20.
点评 本题考查正方形的性质、等腰三角形的性质等知识,解题的关键是学会分类讨论,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
11.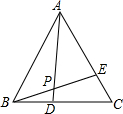 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
8.若某三角形的两边长是3和4,则下列长度的线段能作为其第三边的是( )
| A. | 10 | B. | 9 | C. | 7 | D. | 5 |
5.在下列各实数中,属于无理数的是( )
| A. | 0.23 | B. | -$\frac{22}{7}$ | C. | $\frac{π}{3}$ | D. | $\sqrt{16}$ |
9.下列各式中①$\sqrt{\frac{1}{2}}$,②$\sqrt{2x}$,③$\sqrt{{x}^{3}}$,④$\sqrt{-5}$,⑤$\root{3}{5}$,二次根式的个数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.函数y=$\sqrt{x-6}$的自变量x的取值范围是( )
| A. | x>6 | B. | x<6 | C. | x≥6 | D. | x≤6 |
 将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案,设菱形中较小的角为α度,平行四边形中较大的角为β度,那么β可以用含α的代数式表示为β=$\frac{180+α}{2}$.
将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案,设菱形中较小的角为α度,平行四边形中较大的角为β度,那么β可以用含α的代数式表示为β=$\frac{180+α}{2}$.