题目内容
20. 如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.
如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.求证:BE=BD.
分析 根据等边三角形的性质可得∠CAD=∠DAB=$\frac{1}{2}$∠CAB=30°,AD=AE,∠DAE=60°,再求出∠DAB=∠EAB,然后利用“边角边”证明△ADB与△AEB全等,最后根据全等三角形对应边相等证明即可.
解答 证明:∵在等边△ABC中,点D为边BC的中点,
∴∠CAD=∠DAB=$\frac{1}{2}$∠CAB=30°,
∵△ADE为等边三角形,
∴AD=AE,∠DAE=60°,
∵∠DAB=30°,
∴∠DAB=∠EAB=30°,
在△ADB与△AEB中,$\left\{\begin{array}{l}{AD=AE}\\{∠DAB=∠EAB}\\{AB=AB}\end{array}\right.$,
∴△ADB≌△AEB(SAS),
∴BE=BD.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质,熟记性质以及三角形全等的判定方法并确定出三角形全等的条件是解题的关键.

练习册系列答案
相关题目
15.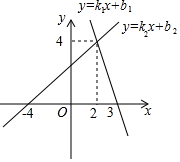 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为( )
如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为( )
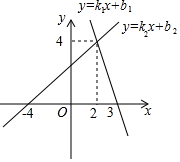 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为( )
如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ |
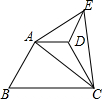 如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.
如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.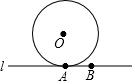 如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.