题目内容
10.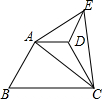 如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.
如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.
分析 根据平行线的性质得到∠BAD=180°-∠B=120°,∠ADE=∠BAD=120°,由三角形内角和定理可求∠BAC,由折叠的性质得∠EAB的度数,再根据角的和差关系可求∠DAE的度数,再由三角形内角和定理可求∠AED的度数.
解答 解:∵AD∥BC,
∴∠BAD=180°-∠B=120°,
∵ED∥AB,
∴∠ADE=∠BAD=120°,
∵∠B=60°,∠ACB=40°,
∴∠BAC=80°,
由折叠的性质得∠EAB=2∠BAC=160°,
∴∠DAE=160°-120°=40°,
∴∠AED=180°-40°-120°=20°.
故答案为:20°.
点评 本题考查了翻折变换(折叠问题),平行线的性质,三角形内角和定理,正确的识别图形是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18.方程组$\left\{\begin{array}{l}{2x+y=□}\\{x+y=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=□}\end{array}\right.$,则被遮盖的两个数分别为( )
| A. | 2,1 | B. | 2,3 | C. | 5,1 | D. | 2,4 |
5. 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )| A. | ($\frac{\sqrt{3}}{2}$)2016 | B. | ($\sqrt{3}$)2016 | C. | 22017 | D. | ($\sqrt{3}$)2017 |
2.下列运算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | (-3)3=27 | C. | $\sqrt{16}$=4 | D. | $\root{3}{9}$=3 |
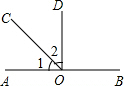 如图,点O在直线AB上,∠1=$\frac{1}{3}$∠BOC,OC是∠AOD的平分线;
如图,点O在直线AB上,∠1=$\frac{1}{3}$∠BOC,OC是∠AOD的平分线; 如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD=$\frac{3}{4}$.
如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD=$\frac{3}{4}$. 如图,小明于堤边A处垂钓,河堤AB的坡比为1:$\sqrt{3}$,坡长为3米,钓竿AC的倾斜角是60°,其长为6米,若钓竿AC与钓鱼线CD的夹角为60°,求浮漂D与河堤下端B之间的距离.
如图,小明于堤边A处垂钓,河堤AB的坡比为1:$\sqrt{3}$,坡长为3米,钓竿AC的倾斜角是60°,其长为6米,若钓竿AC与钓鱼线CD的夹角为60°,求浮漂D与河堤下端B之间的距离. 如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.
如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.