题目内容
2.小明用代入法解二元一次方程组$\left\{\begin{array}{l}{2x-y=3(1)}\\{x+y=-12(2)}\end{array}\right.$第一步:将方程(1)变形得y=2x-3 (3)
第二步:把方程(3)代入方程(1),得2x-(2x-3)=3
第三步:整理得 3=3
第四步:因为x可取一切有理数,所以原方程组有无数个解
问题:①以上解法,造成错误的一步是第二步.
②请你给出用加减消元法解此二元一次方程组的正确过程.
分析 ①第二步应为把(3)代入(2)中;
②利用加减消元法求出解即可.
解答 解:①以上解法,造成错误的一步是第二步;
故答案为:第二步;
②$\left\{\begin{array}{l}{2x-y=3(1)}\\{x+y=-12(2)}\end{array}\right.$,
(1)+(2)得:3x=-9,
解得:x=-3,
把x=-3代入(2)得:y=-9,
则方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-9}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
10.化简$\sqrt{{{(-7)}^2}}$=( )
| A. | -7 | B. | 7 | C. | ±7 | D. | 49 |
14.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等腰直角三角形 | B. | 平行四边形 | C. | 菱形 | D. | 等边三角形 |

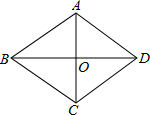 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,BD=6,AC=4,$BC=\sqrt{13}$,四边形ABCD是菱形吗?请说出你的理由.
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,BD=6,AC=4,$BC=\sqrt{13}$,四边形ABCD是菱形吗?请说出你的理由.