题目内容
12.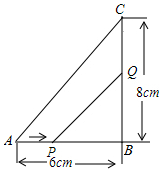 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).(1)如果P、Q分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于是△ABC的三分之一?
(2)如果P、Q两点分别从A、B两点同时出发,而且动点P从A点出发,沿AB移动(到达点B即停止运动),动点Q从B出发,沿BC移动(到达点C即停止运动),几秒钟后,P、Q相距6厘米?
(3)如果P、Q两点分别从A、C两点同时出发,而且动点P从A点出发,沿AB移动(到达点B即停止运动),动点Q从C出发,沿CB移动(到达点B即停止运动),是否存在一个时刻,PQ同时平分△ABC的周长与面积?若存在求出这个时刻的t 值,若不存在说明理由.
分析 (1)设经过t秒钟,△PBQ的面积等于是△ABC的三分之一,根据题意得:AP=t,BP=6-t,BQ=2t,由,△PBQ的面积等于是△ABC的三分之一列式可得求出t的值;
(2)在Rt△PQB中,根据勾股定理列方程即可;
(3)分两种情况:①当PQ平分△ABC面积时,计算出这时的t=5-$\sqrt{13}$,同时计算这时PQ所截△ABC的周长是否平分;②当PQ平分△ABC周长时,计算出这时的t=$\frac{2}{3}$,此时△PBQ的面积是否为$\frac{1}{2}{S}_{△ABC}$,计算即可.
解答 解:(1)设经过t秒钟,△PBQ的面积等于是△ABC的三分之一,
由题意得:AP=t,BP=6-t,BQ=2t,
$\frac{1}{2}$×2t×(6-t)=$\frac{1}{3}$×$\frac{1}{2}$×6×8,
解得:t=2或4,
∵0≤t≤4,
∴t=2或4符合题意,
答:经过2或4秒钟,△PBQ的面积等于是△ABC的三分之一;
(2)在Rt△PQB中,PQ2=BQ2+PB2,
∴62=(2t)2+(6-t)2,
解得:t1=0(舍),t2=$\frac{12}{5}$,
答:$\frac{12}{5}$秒钟后,P、Q相距6厘米;
(3)由题意得:PB=6-t,BQ=8-2t,
分两种情况:
①当PQ平分△ABC面积时,
S△PBQ=$\frac{1}{2}$S△ABC,
$\frac{1}{2}$(6-t)(8-2t)=$\frac{1}{2}$×$\frac{1}{2}$×8×6,
解得:t1=5+$\sqrt{13}$,t2=5-$\sqrt{13}$,
∵Q从C到B,一共需要8÷2=4秒,5+$\sqrt{13}$>4,
∴t1=5+$\sqrt{13}$不符合题意,舍去,
当t2=5-$\sqrt{13}$时,AP=5-$\sqrt{13}$,BP=6-(5-$\sqrt{13}$)=1+$\sqrt{13}$,BQ=8-2(5-$\sqrt{13}$)=2$\sqrt{13}$-2,CQ=2(5-$\sqrt{13}$)=10-2$\sqrt{13}$,
PQ将△ABC的周长分为两部分:
一部分为:AC+AP+CQ=10+5-$\sqrt{13}$+10-2$\sqrt{13}$=25-3$\sqrt{13}$,
另一部分:PB+BQ=1+$\sqrt{13}$+2$\sqrt{13}$-2=3$\sqrt{13}$-1,
25-3$\sqrt{13}$≠3$\sqrt{13}$-1,
②当PQ平分△ABC周长时,
AP+AC+CQ=PB+BQ,
10+2t+t=6-t+8-2t,
t=$\frac{2}{3}$,
当t=$\frac{2}{3}$时,PB=6-$\frac{2}{3}$=$\frac{16}{3}$,
BQ=8-2×$\frac{2}{3}$=$\frac{20}{3}$,
∴S△PBQ=$\frac{1}{2}$×$\frac{16}{3}$×$\frac{20}{3}$=$\frac{160}{3}$≠12,
综上所述,不存在这样一个时刻,PQ同时平分△ABC的周长与面积.
点评 本题是动点运动问题,在三角形中的动点问题,首先要确定两个动点的:路线、路程、速度、时间,表示出时间为t时的路程是哪一条线段的长,根据已知条件列等式或方程,解出即可.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | -$\sqrt{11}$ | B. | $\sqrt{11}$ | C. | -$\sqrt{44}$ | D. | $\sqrt{44}$ |
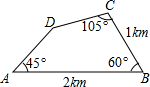 为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )| A. | $\frac{3+\sqrt{6}}{4}$km2 | B. | $\frac{3-\sqrt{6}}{4}$km2 | C. | $\frac{6+\sqrt{3}}{4}$km2 | D. | $\frac{6-\sqrt{3}}{4}$km2 |
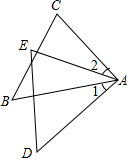 如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.
如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.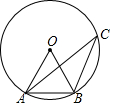 计算:如图,在⊙O中,∠ACB=30°,AB=6.
计算:如图,在⊙O中,∠ACB=30°,AB=6.