题目内容
1.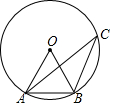 计算:如图,在⊙O中,∠ACB=30°,AB=6.
计算:如图,在⊙O中,∠ACB=30°,AB=6.(1)填空:∠AOB=60°;
(2)求$\widehat{AB}$的长(结果保留π).
分析 (1)根据圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半可得∠AOB=2∠ACB=60°;
(2)利用弧长公式l=$\frac{nπr}{180}$(弧长为l,圆心角度数为n,圆的半径为r)进行计算即可.
解答 解:(1)∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
故答案为:60;
(2)∵∠AOB=60°,
∴${l}_{\widehat{AB}}$=$\frac{60×π×6}{180}$=2π.
点评 此题主要考查了圆周角定理和弧长计算,关键是掌握弧长公式l=$\frac{nπr}{180}$和圆周角定理.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
13.已知直角三角形面积是24平方厘米,斜边长是10厘米,则这个直角三角形两直角边( )
| A. | 6厘米和10厘米 | B. | 8厘米和10厘米 | C. | 6厘米和8厘米 | D. | 8厘米和8厘米 |

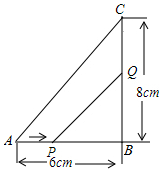 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动). 如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.
如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.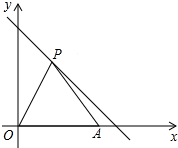 如图,点A坐标为(4,0),点P在第一象限且在直线y=-x+5上.
如图,点A坐标为(4,0),点P在第一象限且在直线y=-x+5上.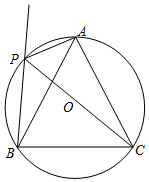 如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.
如图,⊙O是等边三角形ABC的外接圆,点P是$\widehat{AB}$上一点,连接AP,CP,作射线BP.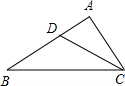 如图,∠ACD=∠B,AC=6,AD=4,则AB=9.
如图,∠ACD=∠B,AC=6,AD=4,则AB=9.