题目内容
4.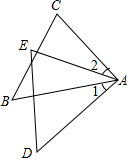 如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.
如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.证明:∵∠1=∠2(已知 ),
∠1+∠EAB=∠2+∠EAB
即∠BAC=∠DAE.
在△ABC和△ADE中,
AB=AD(已知),
∠BAC=∠DAE,
AC=AE(已知),
∴△ABC≌△ADE(SAS)
∴∠C=∠E(全等三角形的对应角相等)
分析 根据已知条件结合图形即可作出解答.
解答 解::∵∠1=∠2( 已知 ),
∠1+∠EAB=∠2+∠EAB,
即∠BAC=∠DAE.
在△ABC和△ADE中
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AC=AE}\end{array}\right.$
∴△ABC≌△ADE(SAS),
∴∠C=∠E(全等三角形的对应角相等)
故答案是:已知;∠EAB;∠EAB;∠DAE;∠BAC=∠DAE;△ABC≌△ADE;SAS;全等三角形的对应角相等.
点评 本题主要考查三角形全等的判定和全等三角形的对应边相等,要牢固掌握并灵活运用这些知识.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
13.已知直角三角形面积是24平方厘米,斜边长是10厘米,则这个直角三角形两直角边( )
| A. | 6厘米和10厘米 | B. | 8厘米和10厘米 | C. | 6厘米和8厘米 | D. | 8厘米和8厘米 |
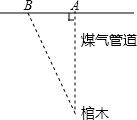 如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?
如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?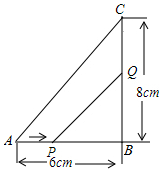 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动). 如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.
如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.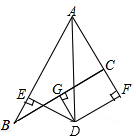 已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.