题目内容
请你判断以n2-1,2n,n2+1(n>1)为边的三角形是否为直角三角形?
考点:勾股定理的逆定理
专题:
分析:证明出(n2-1)2+(2n)2=(n2+1)2即可利用勾股定理逆定理得到以n2-1,2n,n2+1(n>1)为边的三角形是否是直角三角形.
解答:解:∵(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1=(n2+1)2,
∴以n2-1,2n,n2+1(n>1)为边能够成直角三角形.
∴以n2-1,2n,n2+1(n>1)为边能够成直角三角形.
点评:此题主要考查了勾股定理逆定理,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在数轴上,到原点距离5个单位长度,且在数轴右边的数是( )
| A、-5 | B、+5 | C、±5 | D、15 |
若m是一元二次方程x2-5x-2=0的一个实数根,则2014-m2+5m的值是( )
| A、2011 | B、2012 |
| C、2013 | D、2014 |
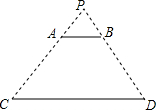 如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则AB与CD的距离是( )m.
如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则AB与CD的距离是( )m. 如图,△ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.
如图,△ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.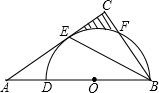 如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 已知CD∥AE,∠1=∠2,∠3=∠4,判断△ABC是否是直角三角形,说明理由.
已知CD∥AE,∠1=∠2,∠3=∠4,判断△ABC是否是直角三角形,说明理由.