题目内容
19.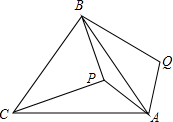 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为24+9$\sqrt{3}$.
分析 连结PQ,如图,根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得AP=PQ=6,∠PAQ=60°,则可判断△APQ为等边三角形,所以PQ=AP=6,接着证明△APC≌△ABQ得到PC=QB=10,然后利用勾股定理的逆定理证明△PBQ为直角三角形,再根据三角形面积公式,利用S四边形APBQ=S△BPQ+S△APQ进行计算.
解答 解:连结PQ,如图,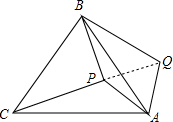 ∵△ABC为等边三角形,
∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵线段AP绕点A顺时针旋转60°得到线段AQ,
∴AP=PQ=6,∠PAQ=60°,
∴△APQ为等边三角形,
∴PQ=AP=6,
∵∠CAP+∠BAP=60°,∠BAP+∠BAQ=60°,
∴∠CAP=∠BAQ,
在△APC和△ABQ中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAP=∠BAQ}\\{AP=AQ}\end{array}\right.$,
∴△APC≌△ABQ,
∴PC=QB=10,
在△BPQ中,∵PB2=82=64,PQ2=62,BQ2=102,
而64+36=100,
∴PB2+PQ2=BQ2,
∴△PBQ为直角三角形,∠BPQ=90°,
∴S四边形APBQ=S△BPQ+S△APQ=$\frac{1}{2}$×6×8+$\frac{\sqrt{3}}{4}$×62=24+9$\sqrt{3}$.
故答案为24+9$\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和等边三角形的性质.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
10.若不等式组$\left\{\begin{array}{l}{x<2a-1}\\{x>3}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤2 | B. | a>2 | C. | a>3 | D. | a≥3 |
4.下列说法正确的是( )
| A. | 掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件 | |
| B. | 审查书稿中有哪些学科性错误适合用抽样调查法 | |
| C. | 甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为$\frac{1}{2}$ |
8.一元二次方程(x+1)2-2(x-1)2=7的根的情况是( )
| A. | 无实数根 | B. | 有一正根一负根 | C. | 有两个正根 | D. | 有两个负根 |
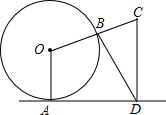 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.
如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.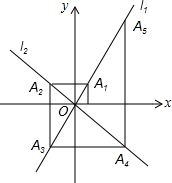 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009). 正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=$\sqrt{2}$.则四边形ABFE′的面积是$\frac{6+3\sqrt{2}}{2}$.
正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=$\sqrt{2}$.则四边形ABFE′的面积是$\frac{6+3\sqrt{2}}{2}$. 如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.