题目内容
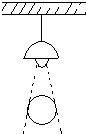 如图,在一间黑暗的屋子里用一盏白炽灯照一个球.
如图,在一间黑暗的屋子里用一盏白炽灯照一个球.(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向高处移时,阴影的大小怎样变化?
(3)若自炽灯到球心的距离是1m,到地面的距离是3m,球的半径是0.2m,问:球在地面上阴影的面积是多少?
考点:视点、视角和盲区
专题:
分析:(1)球在灯光的正下方,所以阴影是圆形;
(2)根据中心投影的特点可知:在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以白炽灯向上移时,阴影会逐渐变小;
(3)先根据相似求出阴影的半径,再求面积.
(2)根据中心投影的特点可知:在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以白炽灯向上移时,阴影会逐渐变小;
(3)先根据相似求出阴影的半径,再求面积.
解答:解:(1)因为球在灯光的正下方,所以阴影是圆形;
(2)白炽灯向上移时,阴影会逐渐变小;
(3)设球在地面上阴影的半径为x米,

则
=
,
解得:x2=
,
则S阴影=
π(平方米).
(2)白炽灯向上移时,阴影会逐渐变小;
(3)设球在地面上阴影的半径为x米,

则
| ||
| 3 |
| 0.2 |
| x |
解得:x2=
| 3 |
| 8 |
则S阴影=
| 3 |
| 8 |
点评:本题考查了中心投影的特点和规律以及相似形性质的运用.解题的关键是利用中心投影的特点可知在这两组圆形相似,利用其相似比作为相等关系求出所需要的阴影的半径,从而求出面积.

练习册系列答案
相关题目
多项式-4a2b2+12a2b3-8a3b2c的公因式是( )
| A、-4a2b2c |
| B、-a2b2 |
| C、-4a3b2c |
| D、-4a2b2 |
 如图,在正方形ABCD中,E为AD的中点,F是BA延长线上一点,AF=
如图,在正方形ABCD中,E为AD的中点,F是BA延长线上一点,AF= 如图是一个粮仓(圆锥与圆柱组合体)的示意图,请画出它的三视图.
如图是一个粮仓(圆锥与圆柱组合体)的示意图,请画出它的三视图. 如图,在?ABCD中,对角线AC与BD交于点O,OE⊥AC交AD于点E,△CDE的周长为12,求?ABCD的周长.
如图,在?ABCD中,对角线AC与BD交于点O,OE⊥AC交AD于点E,△CDE的周长为12,求?ABCD的周长.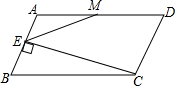 如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM.
如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM.