Question

11．如图，己知抛物线y=x²+bx+c图象经过点以（-1，0），B（0，-3），抛物线与x轴的另一个交点为C．
（1）求这个抛物线的解析式：
（2）若抛物线的对称轴上有一动点D，且△BCD为等腰三角形（CB≠CD），试求点D的坐标；
（3）若点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q也在直线BC上，且PQ=$\sqrt{2}$，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．

Answer 1

分析 （1）将（-1，0），B（0，-3）代入抛物线的解析式可求得b、c的值；
（2）抛物线的对称轴为x=1，然后再求得点C的坐标，设点D的坐标为（1，a），依据两点间的距离公式分别求得BD、BC、CD的长，然后分为BD=BC和DC=DB两种情况列方程求解即可；
（3）先求得∠MPN=45°，设直线BC的解析式为y=kx+b，将点B和点C的坐标代入可求得BC的解析式，当t＜0时点P在线段CB的延长线上，过点M作MN⊥BC，垂足为N．设点P的坐标为（t，t-3），则M的坐标为（t，t²-2t-3），则MP=t²-3t，然后依据MN=sin45°•MP可表示出MN的长，最后依据三角形的面积公式可求得S与t的关系式，同理可求得点P在线段BC上和点P在线段BC的延长线上时，S与t的函数关系式．

解答 解：（1）将（-1，0），B（0，-3），代入抛物线的解析式得：$\left\{\begin{array}{l}{1-b+c=0}\\{c=-3}\end{array}\right.$，
解得：b=-2，c=-3．
∴抛物线的解析式为y=x²-2x-3．

（2）抛物线的对称性为x=-$\frac{b}{2a}$=1，
令y=0得：x²-2x-3=0，解得x=-1或x=3，
∴C（3，0）．
设点D的坐标为（1，a）．
当BD=BC时，依据两点间的距离公式可知：1²+（a+3）²=3²+3²，解得：x=-3+$\sqrt{17}$或x=-3-$\sqrt{17}$．
∴点D的坐标为（1，-3+$\sqrt{17}$），（1，-3-$\sqrt{17}$）．
当DC=DB时，依据两点间的距离公式可知：2²+a²=1²+（a+3）²，解得：a=-1，
∴点D的坐标为（1，-1）．

（3）∵OC=OB，∠COB=90°，
∴∠MPN=45°．
设直线BC的解析式为y=kx+b，将点B和点C的坐标代入直线BC的解析式得：$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$，解得：k=1，b=-3．
∴直线BC的解析式为y=x-3．
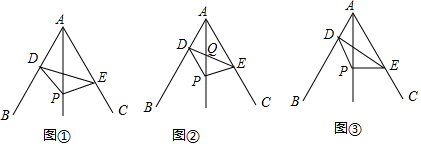
如图1所示：当t＜0时点P在线段CB的延长线上，过点M作MN⊥BC，垂足为N．

设点P的坐标为（t，t-3），则M的坐标为（t，t²-2t-3），则MP=t²-2t-3-（t-3）=t²-3t．
∴MN=sin45°•MP=$\frac{\sqrt{2}}{2}$t²-$\frac{3\sqrt{2}}{2}$t．
∴△PQM的面积=$\frac{1}{2}$PQ•MN=$\frac{1}{2}$×$\sqrt{2}$×（$\frac{\sqrt{2}}{2}$t²-$\frac{3\sqrt{2}}{2}$t）=$\frac{1}{2}$t²-$\frac{3}{2}$t．
∴当t＜0时，S=$\frac{1}{2}$t²-$\frac{3}{2}$t．
如图所示：当0＜t＜3时，点P在线段BC上，过点P作PN⊥BC，垂足为N．

设点P的坐标为（t，t-3），则M的坐标为（t，t²-2t-3），则MP=t-3-（t²-2t-3）=-t²+3t．
∴MN=sin45°•MP=-$\frac{\sqrt{2}}{2}$t²+$\frac{3\sqrt{2}}{2}$t．
∴△PQM的面积=$\frac{1}{2}$PQ•MN=$\frac{1}{2}$×$\sqrt{2}$×（-$\frac{\sqrt{2}}{2}$t²+$\frac{3\sqrt{2}}{2}$t）=-$\frac{1}{2}$t²+$\frac{3}{2}$t．
∴当0＜t＜3时，S=-$\frac{1}{2}$t²+$\frac{3}{2}$t．
如图3所示，当t＞3时，点P在BC的延长线上，过点M作MN⊥BC，垂足为C．

设点P的坐标为（t，t-3），则M的坐标为（t，t²-2t-3），则MP=t²-2t-3-（t-3）=t²-3t．
∴MN=sin45°•MP=$\frac{\sqrt{2}}{2}$t²-$\frac{3\sqrt{2}}{2}$t．
∴△PQM的面积=$\frac{1}{2}$PQ•MN=$\frac{1}{2}$×$\sqrt{2}$×（$\frac{\sqrt{2}}{2}$t²-$\frac{3\sqrt{2}}{2}$t）=$\frac{1}{2}$t²-$\frac{3}{2}$t．
∴当t＞3时，S=$\frac{1}{2}$t²-$\frac{3}{2}$t．
综上所述，S与t的函数关系式为S=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}-\frac{3}{2}t（t＜0或t＞3）}\\{-\frac{1}{2}{t}^{2}+\frac{3}{2}t（0＜t＜3）}\end{array}\right.$．

点评 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系法求一次函数、二次函数的解析式、两点间的距离公式、二次函数的性质，分类讨论是解题的关键．