题目内容
8.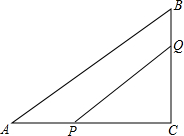 如图,△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从A点出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,当其中一点首先到达终点时运动停止,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的$\frac{2}{3}$?
如图,△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从A点出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,当其中一点首先到达终点时运动停止,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的$\frac{2}{3}$?
分析 设点P,Q出发x秒后可使四边形APQB是△ABC面积的$\frac{2}{3}$,AP=2xcm,PC=(8-2x)cm,CQ=(6-x)cm,此时△PCQ的面积为:$\frac{1}{2}$×(8-2x)(6-x),令该式=$\frac{2}{3}$×24,由此等量关系列出方程求出符合题意的值.
解答 解:设点P,Q出发x秒后可使四边形APQB是△ABC面积的$\frac{2}{3}$,
∵∠C=90°,AB=10cm,AC=8cm,
∴BC=6cm,
由题意得:
S△ABC=$\frac{1}{2}$×AC•BC=$\frac{1}{2}$×6×8=24(cm2),
即:24-$\frac{1}{2}$×(8-2x)×(6-x)=$\frac{2}{3}$×24,
x2-10x+16=0,
(x-2)(x-8)=0,
x1=8(舍去),x2=2.
答:点P,Q出发2秒后可使四边形APQB是△ABC面积的$\frac{2}{3}$.
点评 此题主要考查了一元二次方程的应用,关键在于表示出三角形面积进而得出等量关系求解.

练习册系列答案
相关题目
19.下列各个数中,是无理数的有( )
$\sqrt{2}$,$\root{3}{1000}$,π,-3.1416,$\sqrt{9}$,$\frac{1}{3}$,0.030030003…,0.57143,$\root{3}{-1}$.
$\sqrt{2}$,$\root{3}{1000}$,π,-3.1416,$\sqrt{9}$,$\frac{1}{3}$,0.030030003…,0.57143,$\root{3}{-1}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.已知x1、x2是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-1,则m的值是( )
| A. | 3 | B. | 3或-1 | C. | 1 | D. | -3或1 |
3. 有理数a,b在数轴上对应点的位置如图所示,则( )
有理数a,b在数轴上对应点的位置如图所示,则( )
 有理数a,b在数轴上对应点的位置如图所示,则( )
有理数a,b在数轴上对应点的位置如图所示,则( )| A. | ab>0 | B. | a+b>0 | C. | |b|>1 | D. | a-b<0 |
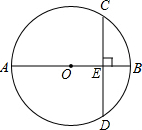 如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm.
如图:⊙O的直径AB⊥CD于E,若BE=4cm,CD=16cm.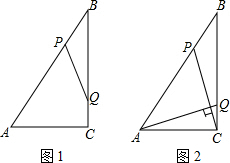 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ. 如图,已知∠AOB=90°,求∠ACB的度数.
如图,已知∠AOB=90°,求∠ACB的度数.