题目内容
11.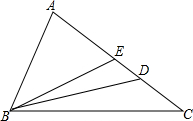 如图,D为AC上一点,E为AD一点,且AD=AB,∠EBD=∠DBC.求证:
如图,D为AC上一点,E为AD一点,且AD=AB,∠EBD=∠DBC.求证:(1)△ABE∽△ACB;
(2)AD2=AE•AC.
分析 (1)由AB=AD,得到∠1+∠5=∠4,根据外角的性质得到∠3=∠1+∠4,于是得到∠3=∠1+∠1+∠5=∠2+∠1+∠5,推出∠3=∠ABC,即可得到结论;
(2)根据相似三角形的性质得到$\frac{AB}{AC}=\frac{AE}{AB}$,于是得到AB2=AC•AE,等量代换即可得到结论.
解答 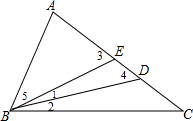 证明:(1)∵∠EBD=∠DBC,
证明:(1)∵∠EBD=∠DBC,
∴∠1=∠2,
∵AB=AD,
∴∠1+∠5=∠4,
∵∠3=∠1+∠4,
∴∠3=∠1+∠1+∠5=∠2+∠1+∠5,
即∠3=∠ABC,
∵∠A=∠A,
∴△ABE∽△ACB;
(2)∵△ABE∽△ACB,
∴$\frac{AB}{AC}=\frac{AE}{AB}$,
∴AB2=AC•AE,
∵AB=AD,
∴AD2=AE•AC.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
19.下列各个数中,是无理数的有( )
$\sqrt{2}$,$\root{3}{1000}$,π,-3.1416,$\sqrt{9}$,$\frac{1}{3}$,0.030030003…,0.57143,$\root{3}{-1}$.
$\sqrt{2}$,$\root{3}{1000}$,π,-3.1416,$\sqrt{9}$,$\frac{1}{3}$,0.030030003…,0.57143,$\root{3}{-1}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.已知x1、x2是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-1,则m的值是( )
| A. | 3 | B. | 3或-1 | C. | 1 | D. | -3或1 |
3. 有理数a,b在数轴上对应点的位置如图所示,则( )
有理数a,b在数轴上对应点的位置如图所示,则( )
 有理数a,b在数轴上对应点的位置如图所示,则( )
有理数a,b在数轴上对应点的位置如图所示,则( )| A. | ab>0 | B. | a+b>0 | C. | |b|>1 | D. | a-b<0 |
1.云浮市的移动手机收费如表,用户可任选其一:
(1)某用户某月用手机通话x小时,请你分别写出A,B两种套餐下该用户在该月应交付的费用;
(2)若某用户估计一个月内用手机通话15小时,你认为选用哪种套餐更合算?
| 月租(元) | 每分钟(元) | |
| A套餐 | 14 | 0.1 |
| B套餐 | 0 | 0.25 |
(2)若某用户估计一个月内用手机通话15小时,你认为选用哪种套餐更合算?
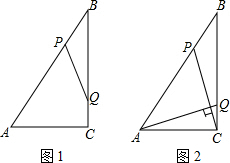 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.