Question

19．如图，一梯子AB斜靠在与地面垂直的墙上，顶端A到墙角C的距离AC=8米，点P为梯子的中点，
（1）若梯子的顶端A下滑2米，底端B恰好向外滑行2米，求梯子AB的长；
（2）若梯子AB沿墙下滑，则在下滑的过程中，点P到墙角C的距离是否发生变化？并说明理由．

Answer 1

分析 （1）设BC=x米，根据勾股定理得出方程，解方程求出BC，再由勾股定理求出AB即可；
（2）由直角三角形斜边上的中线性质得出CP=$\frac{1}{2}$AB=5米；即可得出结论．

解答 解：如图所示：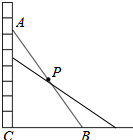
（1）设BC=x米，
根据题意得：8²+x²=6²+（x+2）²，
解得：x=6，
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10（米）；
答：梯子AB的长为6米；
（2）点P到墙角C的距离不发生变化；理由如下：
∵在Rt△ABC中，P为AB的中点，
∴CP=$\frac{1}{2}$AB=5米；
答：在下滑的过程中，点P到墙角C的距离不发生变化．

点评 本题考查了勾股定理的应用、直角三角形斜边上的中线性质；熟练掌握勾股定理，由勾股定理求出梯子AB的长是解决问题的关键．