题目内容
12．
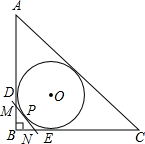如图，Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D，E，如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D，E，过劣弧DE（不包括端点D，E）上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为2，则Rt△MBN的周长为4．
分析 证明四边形DBEO是正方形，然后根据切线长定理证明Rt△MBN的周长等于BD+BE即可求解．
解答 解：连接OD、OE．
∵AB和BC是⊙O的切线，
∴OD⊥AB，OE⊥BC，BD=BE，
则四边形DBEO是正方形．
∴BD=BE=2，
又∵MN是切线，
∴MP=MD，NP=NE，
∴Rt△MBN的周长=BM+BN+MN=BM+BN+MP+NP=BM+BN+DM+NE=BD+BE=4．
故答案是：4．
点评 本题考查了切线长定理和切线的性质，证明Rt△MBN的周长等于BD+BE是关键．
练习册系列答案
阅读快车系列答案
相关题目
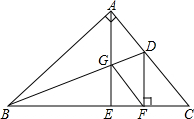如图，在△ABC中，∠BAC=90°，在BC上截取BF=BA，作DF⊥BC交AC于D点，AE⊥BC于E点，交BD于G点，连接GF，求证：DG平分∠AGF．
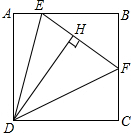如图，正方形ABCD中，点E、F分别在AB、BC上，DH⊥EF于H，DA=HD，EH=2，HF=3．则正方形ABCD的边长为6．
17．观察下表，确定一元二次方程x2-2x-2=0的一个近似根．
| x | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 |
| x2-2x-2 | -1.79 | -1.56 | -1.31 | -1.04 | -0.75 | -0.44 | -0.11 | 0.24 |