题目内容
3.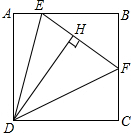 如图,正方形ABCD中,点E、F分别在AB、BC上,DH⊥EF于H,DA=HD,EH=2,HF=3.则正方形ABCD的边长为6.
如图,正方形ABCD中,点E、F分别在AB、BC上,DH⊥EF于H,DA=HD,EH=2,HF=3.则正方形ABCD的边长为6.
分析 设正方形的边长为a,由“HL”可证Rt△ADE≌Rt△HDE,得出AE=EH,同理Rt△CDF≌Rt△HDF,得出CF=HF=3,得出BE=a-2,BF=a-3,EF=HE+HF=5,在Rt△BEF中,由勾股定理得出方程,解方程求出a即可.
解答 解:设正方形的边长为a,
∵四边形ABCD是正方形,
∴AD=CD,∠A=90°,
∵DH⊥EF,
∴∠DHE=∠DHF=90°,
在Rt△ADE和Rt△HDE中,
$\left\{\begin{array}{l}{DE=DE}\\{AD=HD}\end{array}\right.$,
∴Rt△ADE≌Rt△HDE(HL),
∴AE=EH=2,
同理:Rt△CDF≌Rt△HDF,
∴CF=HF=3,
∴BE=a-2,BF=a-3,EF=HE+HF=5,
在Rt△BEF中,BE2+BF2=EF2,
即(a-2)2+(a-3)2=52,
解得:a=6.
故答案为:6.
点评 本题考查了正方形的性质、全等三角形的判定与性质、勾股定理的运用.关键是利用全等三角形的性质,把条件集中到直角三角形中,运用勾股定理求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
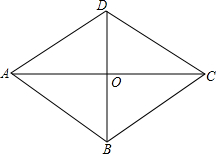 如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒:
如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒: 画出下面几何体的从正面、从左面、从上面看到的形状图.
画出下面几何体的从正面、从左面、从上面看到的形状图.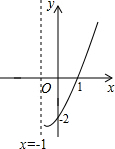 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( ) 玻璃三角板摔成三块如图,若到玻璃店在配一块同样大小的三角板,最省事的方法带③.
玻璃三角板摔成三块如图,若到玻璃店在配一块同样大小的三角板,最省事的方法带③.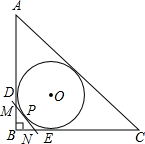 如图,Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D,E,如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为2,则Rt△MBN的周长为4.
如图,Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D,E,如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为2,则Rt△MBN的周长为4.