��Ŀ����
12����֪����������y=$\frac{k-1}{x}$��kΪ������k��1������1����ͼ��������������y=x��ͼ���һ������ΪP������P����������2����k��ֵ��
��2��������ͼ���ÿһ֧�ϣ�y��x���������С����k��ȡֵ��Χ��
��3������ͼ���һ֧λ�ڵڶ����ޣ�����һ֧����ȡ����A��x1��x2����B��x2��y2������y1��y2ʱ���ԱȽ�x1��x2�Ĵ�С��
��4��������ͼ������ȡһ�㣬��x���y�������ߣ������þ������Ϊ6����k��ֵ��
���� ��1�����P������Ϊ��m��2�����ɵ�P������������y=x��ͼ���Ͽ����m��ֵ�������ó�P�����꣬�ٸ��ݵ�P�ڷ���������y=$\frac{k-1}{x}$��ͼ���ϣ�����2=$\frac{k-1}{2}$�����k=5��
��2�������ڷ���������y=$\frac{k-1}{x}$ͼ���ÿһ֧�ϣ�y��x���������С����k-1��0�����k��ȡֵ��Χ���ɣ�
��3������������y=$\frac{k-1}{x}$ͼ���һ֧λ�ڵڶ����ޣ����ڸú���ͼ���ÿһ֧�ϣ�y��x���������������A��x1��y1�����B��x2��y2���ڸú����ĵڶ�����ͼ���ϣ���y1��y2���ʿ�֪x1��x2��
��4�����÷����������ı���ϵ���ļ�������ֱ��д���𰸼��ɣ�
��� �⣺��1�������⣬���P������Ϊ��m��2��
�ߵ�P������������y=x��ͼ���ϣ�
��2=m����m=2��
���P��������2��2����
�ߵ�P�ڷ���������y=$\frac{k-1}{x}$��ͼ���ϣ�
��2=$\frac{k-1}{2}$�����k=5��
��2�����ڷ���������y=$\frac{k-1}{x}$ͼ���ÿһ֧�ϣ�y��x���������С��
��k-1��0�����k��1��
��3���߷���������y=$\frac{k-1}{x}$ͼ���һ֧λ�ڵڶ����ޣ�
���ڸú���ͼ���ÿһ֧�ϣ�y��x�����������
�ߵ�A��x1��y1�����B��x2��y2���ڸú����ĵڶ�����ͼ���ϣ���y1��y2��
��x1��x2��
��4��������ͼ������ȡһ�㣬���������������ߣ��õ��ľ���Ϊ6��
��|k|=6��
��ã�k=��6��
���� ���⿼����Ƿ�����������һ�κ����Ľ������⼰���������������ʣ���֪�������������������ǽ�����Ĺؼ���

| A�� | 3 | B�� | -3 | C�� | 7 | D�� | -7 |
 ��ͼ����1=��2����Ҫʹ��ABD�ա�ACD����Ҫ���ӵ�һ�����������ǣ�������
��ͼ����1=��2����Ҫʹ��ABD�ա�ACD����Ҫ���ӵ�һ�����������ǣ�������| A�� | AB=AC | B�� | BD=CD | C�� | ��BAD=��CAD | D�� | ��B=��C |
 ��ͼ����֪��A��C��E��ͬһֱ���ϣ��������ĸ���ϵʽ�У�ȡ����ʽ����Ϊ���������ĸ�ʽ����Ϊ���ۣ�����һ�������⣬��֤������ȷ��
��ͼ����֪��A��C��E��ͬһֱ���ϣ��������ĸ���ϵʽ�У�ȡ����ʽ����Ϊ���������ĸ�ʽ����Ϊ���ۣ�����һ�������⣬��֤������ȷ��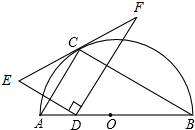 ��ͼ��C����ABΪֱ���İ�Բ��Բ���ϣ���AB=4����ABC=30�㣬DΪ��AB��һ���㣬��E��D����AC�Գƣ���D��A�غ�ʱ��FΪEC���ӳ���������CF=EC�ĵ㣬��D��A���غ�ʱ��FΪEC���ӳ������D�Ҵ�ֱ��DE��ֱ�ߵĽ��㣬
��ͼ��C����ABΪֱ���İ�Բ��Բ���ϣ���AB=4����ABC=30�㣬DΪ��AB��һ���㣬��E��D����AC�Գƣ���D��A�غ�ʱ��FΪEC���ӳ���������CF=EC�ĵ㣬��D��A���غ�ʱ��FΪEC���ӳ������D�Ҵ�ֱ��DE��ֱ�ߵĽ��㣬 ��ͼ1����O�ǵȱ�������ABC�����Բ��P�ǡ�O�ϵ�һ���㣮
��ͼ1����O�ǵȱ�������ABC�����Բ��P�ǡ�O�ϵ�һ���㣮