题目内容
9．若A（5，y1），B（-5，y2）是抛物线y=（x+3）2+k图象上两点，则y1＞y2（填“＞”、“＜”或“=”）．分析 先求得函数y=（x+3）2+k的对称轴为x=-3，再判断A（5，y1）、B（-5，y2）离对称轴的远近，从而判断出y1与y2的大小关系．
解答 解：由y=（x+3）2+k可知抛物线的对称轴为直线x=-3，
∵抛物线开口向上，而点A（5，y1）到对称轴的距离比B（-5，y2）远，
∴y1＞y2．
故答案为＞．
点评 此题主要考查了二次函数图象上点的特征，利用已知解析式得出对称轴进而利用二次函数增减性得出是解题关键．
练习册系列答案
相关题目
19．
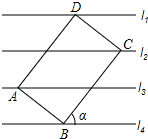已知直线l1∥l2∥l3∥l4，相邻的两条平行线间的距离均为h，矩形ABCD的四个顶点分别在这四条直线上，放置方式如图所示，AB=4，BC=6，则tanα的值等于（ ）
已知直线l1∥l2∥l3∥l4，相邻的两条平行线间的距离均为h，矩形ABCD的四个顶点分别在这四条直线上，放置方式如图所示，AB=4，BC=6，则tanα的值等于（ ）| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
4．若关于x的分式方程$\frac{x-m}{x}$=m-2无解，则m的值为（ ）
| A． | 0 | B． | 0或3 | C． | 3 | D． | ±2 |
14．为了筹备毕业联欢会，班委会对全班同学爱吃哪几种水果作了民意调查，并进行数据整理，在设计买水果的方案时，下面的调查数据中最值得关注的是（ ）
| A． | 平均数 | B． | 加权平均数 | C． | 中位数 | D． | 众数 |
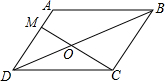如图，在?ABCD中，AM=$\frac{1}{3}$AD，BD与MC相交于点O，则S△MOD：S△COD=2：3．
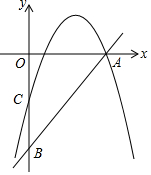如图，直线y=2x-10分别与x轴，y轴交于点A，B，点C为OB的中点，抛物线y=-x2+bx+c经过A，C两点．