题目内容

1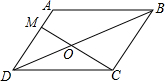．如图，在?ABCD中，AM=$\frac{1}{3}$AD，BD与MC相交于点O，则S△MOD：S△COD=2：3．

分析 首先证明DM：BC=2；3，由DM∥BC，推出DM：BC=OM：OC=2：3，由此即可解决问题．

解答 解：∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∵AM=$\frac{1}{3}$AD，
∴DM：AD=2：3，
∴DM：BC=2；3，
∴DM：BC=OM：OC=2：3，
∴S△MOD：S△COD=2：3，
故答案为2：3．

点评 本题考查平行四边形的性质，平行线分线段成比例定理等知识，解题的关键是灵活运用所学知识解决问题，属于基础题，中考常考题型．

练习册系列答案
相关题目
11．如图，A、B、C是⊙O上的点，若∠AOB=70°，则∠ACB的度数为35°．
12．在数学课上，老师提出如下问题：
如图，AB是⊙O的直径，点C在⊙O外，AC，BC分别与⊙O交于点D，E，请你作出△ABC中BC边上的高．
小文说：连结AE，则线段AE就是BC边上的高．
老师说：“小文的作法正确．”
请回答：小文的作图依据是直径所对的圆周角是直角．
9．若A（5，y1），B（-5，y2）是抛物线y=（x+3）2+k图象上两点，则y1＞y2（填“＞”、“＜”或“=”）．
16．如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A瞬时针旋转到位置①可得到点P1，此时AP1=$\sqrt{2}$；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=1+$\sqrt{2}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=2+$\sqrt{2}$；…，按此规律继续旋转，直至得到点P2017为止，则AP2017=1344+673$\sqrt{2}$．
6．已知1≤a≤$\sqrt{2}$，化简$\sqrt{{a}^{2}-2a+1}$+|a-2|的结果是（　　）
A．2a-3B．2a+3C．1D．3
13．如图，△ABC中，D是AB上一点，已知∠ACD=∠B，AD=4，AB=9，则AC长为（　　）
A．5B．6C．7D．8
10．【问题提出】
学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据斜边直角边对应相等的两个三角形全等，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）已知：△ABC，∠B是锐角，用尺规和圆规作△DEF，使AC=DF，BC=EF，∠B=∠E，且△DEF和△ABC不全等．（不写作法，保留作图痕迹）
（4）在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E，且∠B、∠E都是锐角，∠B与∠A还要满足∠B≥∠A，就可以使△ABC≌△DEF？
11．下列图案中，是中心对称图形的有（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网