题目内容
19.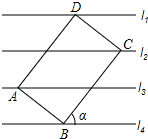 已知直线l1∥l2∥l3∥l4,相邻的两条平行线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα的值等于( )
已知直线l1∥l2∥l3∥l4,相邻的两条平行线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα的值等于( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 过A作AE⊥l4,过C作CF⊥l4,分别交于E、F点,由同角的余角相等得到一对角相等,再由一对直角相等,得到三角形ABE与三角形BCF相似,由相似得比例,表示出BF,在直角三角形BCF中,利用锐角三角函数定义即可求出tanα的值.
解答 解:过A作AE⊥l4,过C作CF⊥l4,分别交于E、F点,
∴∠AEF=∠CFE=90°,
∵矩形ABCD,
∴∠ABC=90°,
∴∠ABE+∠CBF=90°,
∵∠EAB+∠ABE=90°,
∴∠EAB=∠CBF,
∴△ABE∽△CBF,
∵AB=4,BC=6,AE=h,CF=2h,
∴$\frac{AE}{BF}$=$\frac{AB}{BC}$=$\frac{4}{6}$,即BF=$\frac{3}{2}$AE=$\frac{3}{2}$h,
在Rt△BCF中,tanα=$\frac{CF}{BF}$=$\frac{2h}{\frac{3}{2}h}$=$\frac{4}{3}$.
故选D.
点评 此题考查了相似三角形的判定与性质,平行线之间的距离,以及锐角三角函数定义,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
10.如图,下面的四个图形中,线段BE是△ABC的高的图是( )
| A. |  | B. |  | C. |  | D. |  |
7.下面四个图形中,线段BE是△ABC的高的图是( )
| A. |  | B. |  | C. |  | D. |  |
14.9的平方根是( )
| A. | 81 | B. | 3 | C. | ±3 | D. | ±$\sqrt{3}$ |
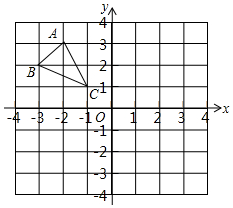 如图,在平面直角坐标中,△ABC各顶点都在小方格的顶点上.
如图,在平面直角坐标中,△ABC各顶点都在小方格的顶点上. 如图,A、B、C是⊙O上的点,若∠AOB=70°,则∠ACB的度数为35°.
如图,A、B、C是⊙O上的点,若∠AOB=70°,则∠ACB的度数为35°.