题目内容
19.若A(2,y1),B($\frac{1}{2}$,y2),C($\sqrt{3}$,y3)三点都在二次函数y=-2x2-6x-c的图象上,则y1,y2,y3的大小关系是y1<y3<y2.分析 求出二次函数的对称轴,再根据二次函数的增减性判断即可.
解答 解:对称轴为直线x=-$\frac{b}{2a}$=-$\frac{3}{2}$,
∵a=-2<0,
∴x<-$\frac{3}{2}$时,y随x的增大而增大,
x>-$\frac{3}{2}$时,y随x的增大而减小,
∵2>$\sqrt{3}$>$\frac{1}{2}$,
∴y1<y3<y2.
故答案为:y1<y3<y2.
点评 本题考查了二次函数图象上点的坐标特征,求出对称轴解析式,然后利用二次函数的增减性求解更简便.

练习册系列答案
相关题目
5.计算:$\sqrt{3}×\sqrt{6}$的结果是( )
| A. | $9\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{6}$ |
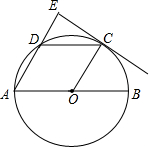 如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$.
如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=$\sqrt{3}$.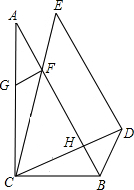 如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号).
如图,Rt△ABC和Rt△CDE中,∠A=30°,∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论:①CH=FH;②BC=GC;③四边形BDEF为平行四边形;④FH=GF+BH.其中正确的结论是①②④(填序号).