题目内容
7．直角三角形的两条直角边长分别为a和b，斜长为c时，则外接圆的半径为$\frac{c}{2}$，内切圆的半径为$\frac{a+b-c}{2}$．分析 由外接圆的圆心在斜边的中点上即可求出外接圆的半径；利用内切圆半径等于两直角边的和与斜边的差的一半，即可计算出内切圆半径．
解答 解：∵直角三角形的两条直角边长分别为a和b，斜长为c，
∴外接圆的半径=$\frac{c}{2}$，内切圆的半径=$\frac{a+b-c}{2}$．
故答案为：$\frac{c}{2}$，$\frac{a+b-c}{2}$．
点评 本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心；三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了三角形的外心性质．记住直角三角形的外接圆半径R和内切圆半径r之间的数量关系是解题关键．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
18．正方形具有而矩形不一定具有的性质是（ ）
| A． | 四个角相等 | B． | 对角线互相垂直 | C． | 对角互补 | D． | 对角线相等 |
15．已知二元一次方程2x+y=8．
（1）填表：
（2）请写出方程2x+y=8的正整数解；
（3）以表格中的数值x，y作为点的横坐标和纵坐标，在平面直角坐标系内描出各点，再顺次连接各点，得到怎样的图形？
（1）填表：
| x | -2 | -1 | 0 | 1 | 2 |
| y | 12 | 10 | 8 | 6 | 4 |
（3）以表格中的数值x，y作为点的横坐标和纵坐标，在平面直角坐标系内描出各点，再顺次连接各点，得到怎样的图形？
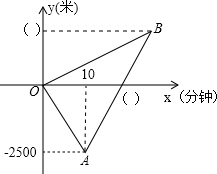早上小芳和妈妈同时从家里出发，小芳步行上学、妈妈骑自行车上班，两人的行进方向正好相反，规定从家往学校的方向为正，如图是她们离家的距离y（米）与时间x（分钟）之间的函数图象，妈妈骑车走了10分钟时接到小芳的电话，立即以原速度前往学校，若已知小芳步行的速度为50米/分钟，并且妈妈与小芳同时到达学校．
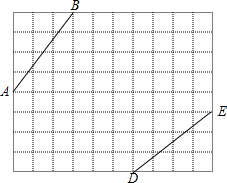如图所示，是10×8的正方形网格，网格中的每个小正方形的边长都是1，线段AB和线段DE的端点都在小正方形的顶点上．
16．不等式x+1＜0的解集在数轴上表示正确的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
