题目内容
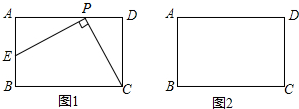
13.提出问题如图1,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的一动点(不与端点A、D重合),连结PC,过点P作PE⊥PC交AB于点E,在P点运动过程中,图中各角和线段之间是否存在的某种关系和规律?
特例求解
当E为AB的中点,且AP>AE时,求证:PE=PC.
深入探究
当点P在AD上运动时,对应的点E也随之在AB上运动,求整个运动过程中BE的取值范围.
分析 特例求解:设AP=x,证明△APE∽△DCP,根据相似三角形的性质得到比例式,解一元二次方程求出x的值,证明△APE≌△DCP即可;
深入探究:设AP=x,AE=y,证明△APE∽△DCP,根据相似三角形的性质得到比例式,计算即可.
解答 解:特例求解,
∵PE⊥PC,
∴∠APE+∠DPC=90°,
∵∠D=90°,
∴∠DCP+∠DPC=90°,
∴∠APE=∠DCP,又∠A=∠D=90°,
∴△APE∽△DCP,
∴$\frac{AP}{DC}$=$\frac{AE}{DP}$,
设AP=x,则DP=3-x,又AE=BE=1,
∴x(3-x)=1×2,
整理得x2-3x+2=0,
解得,x1=2,x2=1,
∵AP>AE,
∴AP=2,AE=PD=1,
∴△APE≌△DCP,
∴PE=PC;
深入探究
设AP=x,AE=y,
∵△APE∽△DCP,
∴$\frac{AP}{DC}$=$\frac{AE}{DP}$,即x(3-x)=2y,
∴y=$\frac{1}{2}$x(3-x)=-$\frac{1}{2}$x2+$\frac{3}{2}$x=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{9}{8}$,
∴当x=$\frac{3}{2}$时,y的最大值为$\frac{9}{8}$,
∵AE=y取最大值时,BE取最小值为2-$\frac{9}{8}$=$\frac{7}{8}$,
∴BE的取值范围为$\frac{7}{8}$≤BE<2.
点评 本题考查的是矩形的性质、相似三角形的判定和性质、全等三角形的判定和性质以及二次函数的解析式的确定以及二次函数的性质,掌握相关的性质定理以及判定定理是解题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
3.下列说法中,正确的是( )
| A. | 64的平方根是8 | B. | 4的平方根是2或-2 | ||
| C. | (-3)2没有平方根 | D. | 16的平方根是4和-4 |
4.在下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.下列关于x的方程,一定是一元二次方程的是( )
| A. | ax2-5x+3=0 | B. | 2x4=5x2 | C. | ${x^2}+\frac{x^2}{x}=1$ | D. | $\frac{1}{2}{x^2}+\sqrt{3}x-4=0$ |
5.下列运算正确的是( )
| A. | a5+a5=a10 | B. | a6×a4=a24 | C. | a+a=2a | D. | a4-a4=a0 |
2.下列计算正确的是( )
| A. | 23÷26=29 | B. | 23-24=2-1 | C. | 23×23=29 | D. | 24÷22=22 |
3.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三内角之比为3:4:5 | B. | 三边之比为1:1:$\sqrt{2}$ | ||
| C. | 三边长分别为5、13、12 | D. | 有两锐角分别为32°、58° |