题目内容
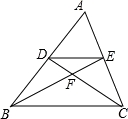
如图,DE∥BC,DF=2,FC=4,那么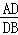 =__________.
=__________.
1.
【考点】相似三角形的判定与性质.
【分析】先根据相似三角形的判定方法可判断△ADE∽△ABC,△DEF∽△CBF,再根据相似三角形的性质得 ,
, ,设AD=k,则AB=2k,可得结果.
,设AD=k,则AB=2k,可得结果.
【解答】解:∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC,
∴ ,
,
∵DE∥BC,
∴∠CDE=∠BCD,∠DEB=∠EBC,
∴△DEF∽△CBF,
∴ ,
,
设AD=k,则AB=2k,BD=2k﹣k=k,
∴ .
.
故答案为:1.
【点评】本题主要考查了相似三角形的判定及性质,能够运用相似三角形的性质得出对应线段成比例是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
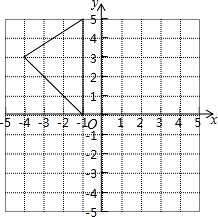
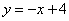 ,当x=1时,y=3;当x=3时,y=1,即当
,当x=1时,y=3;当x=3时,y=1,即当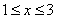 时,有
时,有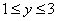 ,所以说函数
,所以说函数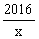 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;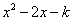 是闭区间[1,2]上的“闭函数”,求k的值;
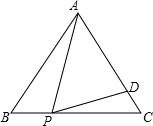
是闭区间[1,2]上的“闭函数”,求k的值; 图,正△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,CD=
图,正△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,CD=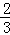 ,则△ABC的边长为__________.
,则△ABC的边长为__________.