题目内容
如图,要在宽为28米的公路AB路边安装路灯,路灯的灯臂CD长为3米,且与灯柱BC成150°角,路灯采用圆锥形灯罩,灯罩的轴线DE与灯臂CD垂直,当灯罩的轴线DE能过公路路面的中点时照效果最理想.问应设计多高的灯柱,才能取得最理想的照明效果.(结果保留根号)
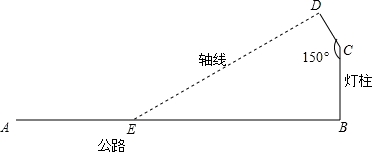
【考点】解直角三角形的应用.
【分析】延长BC、ED交于点F.先解Rt△DCF得到FC=2 米,再解Rt△EBF得到BF=
米,再解Rt△EBF得到BF= 米,利用BC=BF﹣CF代入数据计算即可得到结论.
米,利用BC=BF﹣CF代入数据计算即可得到结论.
【解答】解:延长BC、ED交于点F.
∵∠DCB=150°,
∴∠DCF=30°.
∵∠CDE=90°,
∴∠F=60°.
∵在Rt△DCF中,DC=3,∠DCF=30°,
∴ ,
,
∴ 米,
米,
∵AB=28米,E为AB的中点,
∴BE=14米.
∵在Rt△EBF中,BE=14,∠F=60°,
∴ ,
,
∴ 米,
米,
∴ 米.
米.
答:当灯柱高为 米时能取得最理想的照明效果.
米时能取得最理想的照明效果.

【点评】本题考查了解直角三角形的应用,通过作辅助线构造直角三角形,正确求出BF与CF的值是解题的关键.

练习册系列答案
相关题目
 的解集是 .
的解集是 .


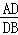 =__________.
=__________.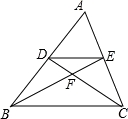

 B.BE=CF C.AC∥DF D.∠ACB=∠DEF
B.BE=CF C.AC∥DF D.∠ACB=∠DEF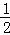 ∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
 轴对称的点的坐标是 .
轴对称的点的坐标是 .