题目内容
9. 已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)k的值是-2;
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=$\frac{-4}{x}$图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{7}{9}$,则b的值是3$\sqrt{2}$.
分析 (1)设出点P的坐标,根据平移的特性写出点Q的坐标,由点P、Q均在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,即可得出关于k、m、n、b的四元一次方程组,两式做差即可得出k值;
(2)根据BO⊥x轴,CE⊥x轴可以找出△AOB∽△AEC,再根据给定图形的面积比即可得出$\frac{AO}{AE}=\frac{BO}{CE}=\frac{3}{4}$,根据一次函数的解析式可以用含b的代数式表示出来线段AO、BO,由此即可得出线段CE、AE的长度,利用OE=AE-AO求出OE的长度,再借助于反比例函数系数k的几何意义即可得出关于b的一元二次方程,解方程即可得出结论.
解答 解:(1)设点P的坐标为(m,n),则点Q的坐标为(m-1,n+2),
依题意得:$\left\{\begin{array}{l}{n=km+b}\\{n+2=k(m-1)+b}\end{array}\right.$,
解得:k=-2.
故答案为:-2.
(2)∵BO⊥x轴,CE⊥x轴,
∴BO∥CE,
∴△AOB∽△AEC.
又∵$\frac{{S}_{1}}{{S}_{2}}$=$\frac{7}{9}$,
∴$\frac{{S}_{△AOB}}{{S}_{△AEC}}$=$\frac{9}{7+9}$=$\frac{9}{16}$.
令一次函数y=-2x+b中x=0,则y=b,
∴BO=b;
令一次函数y=-2x+b中y=0,则0=-2x+b,
解得:x=$\frac{b}{2}$,即AO=$\frac{b}{2}$.
∵△AOB∽△AEC,且$\frac{{S}_{△AOB}}{{S}_{△AEC}}$=$\frac{9}{16}$,
∴$\frac{AO}{AE}=\frac{BO}{CE}=\frac{3}{4}$.
∴AE=$\frac{4}{3}$AO=$\frac{2}{3}$b,CE=$\frac{4}{3}$BO=$\frac{4}{3}$b,OE=AE-AO=$\frac{1}{6}$b.
∵OE•CE=|-4|=4,即$\frac{2}{9}$b2=4,
解得:b=3$\sqrt{2}$,或b=-3$\sqrt{2}$(舍去).
故答案为:3$\sqrt{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数系数k的几何意义以及相似三角形的判定及性质,解题的关键:(1)由P点坐标表示出Q点坐标;(2)找出关于b的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,借助于相似三角形的性质找出各线段的长度,再根据反比例函数系数k的几何意义得出方程是关键.

| A. | -a•a3=a3 | B. | -(a2)2=a4 | C. | x-$\frac{1}{3}$x=$\frac{2}{3}$ | D. | ($\sqrt{3}$-2)($\sqrt{3}$+2)=-1 |
| A. | -3+5 | B. | -3-5 | C. | |-3+5| | D. | |-3-5| |
| A. | (-m-2n) 2n | B. | (m-2n)(2n-m) | C. | (m-2n)(-m-2n) | D. | (2n-m)(-m-2n) |
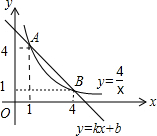 如图,一次函数y=kx+b(k、b为常数,且k≠0)和反比例函数y=$\frac{4}{x}$(x>0)的图象交于A、B两点,利用函数图象直接写出不等式$\frac{4}{x}$<kx+b的解集是1<x<4.
如图,一次函数y=kx+b(k、b为常数,且k≠0)和反比例函数y=$\frac{4}{x}$(x>0)的图象交于A、B两点,利用函数图象直接写出不等式$\frac{4}{x}$<kx+b的解集是1<x<4.