题目内容
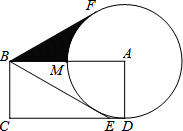 如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.
如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.(1)请判断直线BE与⊙A的位置关系,并说明理由;
(2)如果AB=10,BC=5,求图中阴影部分的面积.
考点:矩形的性质,切线的判定与性质,扇形面积的计算
专题:几何综合题
分析:(1)直线BE与⊙A的位置关系是相切,连接AE,过A作AH⊥BE,过E作EG⊥AB,再证明AH=AD即可;
(2)连接AF,则图中阴影部分的面积=直角三角形ABF的面积-扇形MAF的面积.
(2)连接AF,则图中阴影部分的面积=直角三角形ABF的面积-扇形MAF的面积.
解答: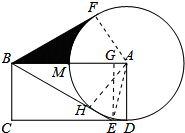 解:(1)直线BE与⊙A的位置关系是相切,
解:(1)直线BE与⊙A的位置关系是相切,
理由如下:连接AE,过A作AH⊥BE,过E作EG⊥AB,则四边形ADEG是矩形.
∵S△ABE=
BE•AH=
AB•EG,AB=BE,
∴AH=EG,
∵四边形ADEG是矩形,
∴AD=EG,
∴AH=AD,
∴BE是圆的切线;
(2)连接AF,
∵BF是⊙A的切线,
∴∠BFA=90°
∵BC=5,
∴AF=5,
∵AB=10,
∴∠ABF=30°,
∴∠BAF=60°,
∴BF=
AF=5
,
∴图中阴影部分的面积=直角三角形ABF的面积-扇形MAF的面积=
×5×5
-
=
.
 解:(1)直线BE与⊙A的位置关系是相切,
解:(1)直线BE与⊙A的位置关系是相切,理由如下:连接AE,过A作AH⊥BE,过E作EG⊥AB,则四边形ADEG是矩形.
∵S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AH=EG,
∵四边形ADEG是矩形,
∴AD=EG,
∴AH=AD,
∴BE是圆的切线;
(2)连接AF,
∵BF是⊙A的切线,
∴∠BFA=90°
∵BC=5,
∴AF=5,
∵AB=10,
∴∠ABF=30°,
∴∠BAF=60°,
∴BF=
| 3 |
| 3 |
∴图中阴影部分的面积=直角三角形ABF的面积-扇形MAF的面积=
| 1 |
| 2 |
| 3 |
| 60•π×52 |
| 360 |
75
| ||
| 6 |
点评:本题考查了矩形的性质、切线的判定和性质、三角形和扇形面积公式的运用以及特殊角的锐角三角函数值,题目的综合性较强,难度不小,解题的关键是正确做出辅助线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在梯形ABCD中,AD∥BC,对角线AC=5,BD=12,AD+BC=13.求证:AC⊥BD.
在梯形ABCD中,AD∥BC,对角线AC=5,BD=12,AD+BC=13.求证:AC⊥BD.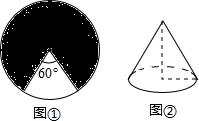 如图,小红同学在半径为4的圆中,剪去一个圆心角为60°的扇形,并将剩下部分(图中阴影部分)制成一个无缝隙且不重合的圆锥,则这个圆锥的高为
如图,小红同学在半径为4的圆中,剪去一个圆心角为60°的扇形,并将剩下部分(图中阴影部分)制成一个无缝隙且不重合的圆锥,则这个圆锥的高为