题目内容
已知m，n为有理数，且m2+2n2-2mn+8n+16=0，求m、n的值．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：据m2+2n2-2mn+8n+16=0，得出（m-n）2+（n+4）2=0，再利用非负数的性质得出m、n的值．
解答：解：∵m2+2n2-2mn+8n+16=0，
∴（m-n）2+（n+4）2=0，
∴m-n=0，n+4=0
解得m=n=-4．
∴（m-n）2+（n+4）2=0，
∴m-n=0，n+4=0
解得m=n=-4．
点评：本题考查了配方法的应用和非负数的性质；关键是根据完全平方公式分组分解因式．
练习册系列答案
相关题目
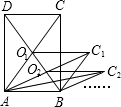如图，矩形ABCD的面积为5，它的两条对角线交于点O1，以AB、AO1为两邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交于点O2，同样以AB、AO2为两邻边作平行四边形ABC2O2，…，依此类推，则平行四边形ABCnOn的面积为（ ）
如图，已知抛物线y=ax2+4ax+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上．
如图是由几个小立方体所搭几何体的俯视图，小正方体的数字表示在该位置的小立方体的个数，请你画出这个几何体的主视图和左视图．