题目内容
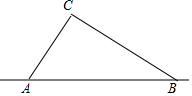
3．
如图，AB∥CD，BC平分∠ACD，若∠1=54°，则∠2=63°．
分析 由AB∥CD，根据平行线的性质得到∠ACD的度数，由BC平分∠ACD，根据角平分线的定义即可得出∠BCD，再结合平行线的性质即可得出结论．
解答 解：∵AB∥CD，∠1=∠BAC=54°，
∴∠ACD=180°-54°=126°，
又∵BC平分∠ACD，
∴∠BCD=63°．
∵AB∥CD，
∴∠2=∠BCD=63°．
故答案为：63°．
点评 本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等；两直线平行，同旁内角互补．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力．如图，有一台风中心沿东西方向AB由点A行驶向点B，已知点C为一海港，且点 C与直线 AB上两点A，B的距离分别为300km和400km，又AB=500km，以台风中心为圆心周围250km以内为受影响区域．
11．与分式$\frac{-a+b}{-a-b}$相等的是（ ）
| A． | $\frac{a+b}{a-b}$ | B． | $\frac{a-b}{a+b}$ | C． | -$\frac{a+b}{a-b}$ | D． | -$\frac{a-b}{a+b}$ |
如图，动点A在曲线y=$\frac{2}{x}$（x＞0）上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC，直线DE分别交x轴，y轴于点M，N，当NE：DM=1：2时，图中的阴影部分的面积等于$\frac{3\sqrt{2}}{2}$．
如图，在平面直角坐标系中，一次函数y=kx+b（k＜0）的图象经过点A．当y＜3时，x的取值范围是x＞2．
如图，正方形ABCD的边长为15，AG=CH=12，BG=DH=9，连接GH，则线段GH的长为3$\sqrt{2}$．
如图，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F，且AF=BD，连结BF．