题目内容
18.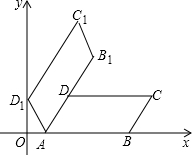 如图,?ABCD的顶点A,B的坐标分别为(1,0),(5,0),∠DAB=60°,AD=2.
如图,?ABCD的顶点A,B的坐标分别为(1,0),(5,0),∠DAB=60°,AD=2.(1)求点D的坐标;
(2)若将?ABCD绕顶点A逆时针旋转60°,得到?AB1C1D1,点D1落在y轴上,AB1经过点D,求点C1的坐标及C1C的长度.
分析 (1)作DM⊥OB于M,求出∠ADM=30°,得出AM=$\frac{1}{2}$AD=1,DM=$\sqrt{3}$AM=$\sqrt{3}$,求出OM=2,即可得出点D的坐标;
(2)作C1G⊥x轴于G,连接C1C,求出C1G=3$\sqrt{3}$,得出点C1的坐标为(2,3$\sqrt{3}$);证出点D在C1G上,且C1D⊥CD,1D=2$\sqrt{3}$,由勾股定理即可求出C1C的长.
解答 解: (1)作DM⊥OB于M,如图1所示:
(1)作DM⊥OB于M,如图1所示:
∵∠DAB=60°,
∴∠ADM=30°,
∴AM=$\frac{1}{2}$AD=1,DM=$\sqrt{3}$AM=$\sqrt{3}$,
∵OA=1,
∴OM=2,
∴点D的坐标为(2,$\sqrt{3}$);
(2)作C1G⊥x轴于G,连接C1C,如图2所示:
∵AD=2,AB1=4,
∴DB1=2=AD=C1B1,
∴C1D=2DG=2$\sqrt{3}$,
∴C1G=3$\sqrt{3}$,
∴点C1的坐标为(2,3$\sqrt{3}$);
∵点D和点C1的横坐标都是2,
∴点D在C1G上,且C1D⊥CD,C1D=2$\sqrt{3}$,
∴C1C=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2$\sqrt{7}$.
点评 本题考查了平行四边形的性质、坐标与图形性质、勾股定理;熟练掌握平行四边形的性质和勾股定理是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
6.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为( )
| A. | 50元、150元 | B. | 50元、100元 | C. | 100元、50元 | D. | 150元、50元 |
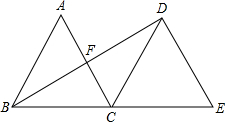 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.