题目内容
3.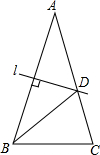 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 75° |
分析 根据三角形的内角和定理,求出∠C,再根据线段垂直平分线的性质,推得∠A=∠ABD=30°,由外角的性质求出∠BDC的度数,从而得出∠CBD=45°.
解答 解:∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∵AB的垂直平分线交AC于D,
∴AD=BD,
∴∠A=∠ABD=30°,
∴∠BDC=60°,
∴∠CBD=180°-75°-60°=45°.
故选B.
点评 此题主要考查线段的垂直平分线的性质和等腰三角形的性质;利用三角形外角的性质求得求得∠BDC=60°是解答本题的关键.本题的解法很多,用底角75°-30°更简单些.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.阅读下列材料:
为了了解某市初中生的视力情况,随机抽取了3000名学生进行检测,收集数据后,绘制了以下三幅统计图表,请根据图表中提供的信息解答下列问题:
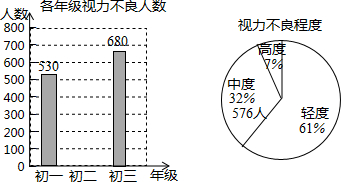
根据统计图表回答下列问题:
(1 )统计表中m=1050,n=66%;
(2)补全条形统计图,并通过计算估计该市80000名初中生的视力不良情况的人数;
(3)通过统计图表中的信息,写出一条关于视力不良的正确结论.
为了了解某市初中生的视力情况,随机抽取了3000名学生进行检测,收集数据后,绘制了以下三幅统计图表,请根据图表中提供的信息解答下列问题:
| 调查人数 | 视力不良 | 视力不良率(精确到0.01) | |
| 男生 | 1400 | 750 | 54% |
| 女生 | 1600 | m | n |

根据统计图表回答下列问题:
(1 )统计表中m=1050,n=66%;
(2)补全条形统计图,并通过计算估计该市80000名初中生的视力不良情况的人数;
(3)通过统计图表中的信息,写出一条关于视力不良的正确结论.
11.下列运算错误的是( )
| A. | ($\sqrt{3}$-1)0=1 | B. | (-3)2÷$\frac{9}{4}$=$\frac{1}{4}$ | C. | 5x2-6x2=-x2 | D. | (2m3)2÷(2m)2=m4 |
18.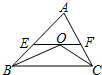 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )| A. | 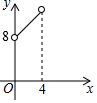 | B. | 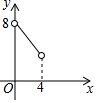 | C. | 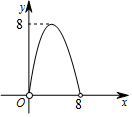 | D. | 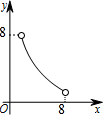 |
15.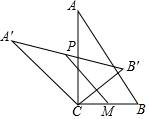 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
12.不等式3x+6≥9的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
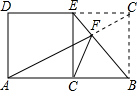 如图所示,在矩形ABCD中,∠DAC=65°,点E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=40°.
如图所示,在矩形ABCD中,∠DAC=65°,点E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=40°.